- Osnovno
- I
Godine učenja i podučavanja predmeta: 1 A
Skupovi, brojevi i operacijeA.I.1 Učenik opisuje svojstva i odnose skupova.
A.I.2 Učenik čita i piše brojeve do 10.
MTP-1.1.1 MTP-1.1.2 - prepoznaje i imenuje elemente skupa
- oblikuje skup sa zadanim elementima
- određuje pripadnost/nepripadnost skupu
- pridružuje elemente skupu
- određuje broj elemenata skupa
- predstavlja skup crtežom.
- prepoznaje oznake za brojeve
- povezuje količinu i broj
- zapisuje i čita brojeve od 1 do 10
- prepoznaje brojevni niz
- broji do 10 unaprijed i unatrag
- predstavlja brojeve na brojevnoj crti
- zapisuje i čita redne brojeve od 1. do 10.
- prepoznaje nulu (0) kao broj elemenata praznog skupa.
- skup
- elementi skupa
- broj elemenata skupa.
- broj
- brojevi od 1 do 10
- brojanje
- brojevna crta, ispred, između, iza
- redni brojevi
- broj nula (0).
Pronalaziti u okruženju/učionici predmete koji imaju zajednička svojstva i formirati skupove. Dodaje i oduzima elemente iz skupa.
Poželjno je naglasiti kako je skup bilo koja kolekcija predmeta iz okruženja/učionice, ne nužno samo onih s istim svojstvima.
Poticati učenike na pravilno korištenje pojmova "pripada", "ne pripada", "element skupa" i "nije element skupa".
Broj elemenata skupa određivati na razini više, manje ili jednako.
Sadržaj ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Priroda i društvo (članovi moje obitelji), Likovna kultura (skupljeno-raspršeno) i Tjelesna i zdravstvena kultura (ekipne igre).
Igrati različite igre: učenici odgovaraju na pitanje koliko čega ima (jedna glava, dvije ruke, tri praseta, četiri sestre, sedam patuljaka, deset prstiju...).
Uspoređivati količinu (više, manje, jednako).
Učenici u redu određuju tko je prvi, drugi, treći,.., deseti itd.
Igrati igru u kojoj se nula javlja kao rješenje ili kao odgovor na pitanje.
Rastavljati brojeve na dva pribrojnika, npr. 7 jabuka čine 4 jabuke i 3 jabuke, ali pritom još ne uvoditi pojmove kao što su plus, zbroj, pribrojnici i sl.
Pridruživati broj broju elemenata skupa.
Sadržaj ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Hrvatski jezik (pisanje brojevne riječi), Priroda i društvo (članovi moje obitelji) i Glazbena kultura (pjevanje brojalica).
C
Geometrija i mjerenjaC.I.1 Učenik uspoređuje predmete po određenom kriteriju.
C.I.2 Učenik određuje odnose među predmetima.
C.I.3 Učenik razlikuje predmete različitih oblika.
MTP-3.1.1 MTP-3.1.1 MTP-3.1.3 - imenuje svojstvo predmeta po boji, duljini, visini i širini
- uspoređuje dva predmeta po duljini, visini i širini
- reda predmete prema zadanom uzorku.
- imenuje odnose među predmetima
- identificira položaj predmeta u odnosu na sebe
- opisuje položaj jednog predmeta u odnosu na drugi.
- imenuje kuglu, valjak, kocku, kvadar, stožac i piramidu
- prepoznaje sličnost predmeta različitih oblika s predmetima u okruženju, na modelima geometrijskih tijela i na ilustracijama
- razlikuje predmete različitih veličina u različitim položajima
- uspoređuje različite predmete.
- boja, duljina, visina i širina
- veliko - malo, usko - široko, visoko - nisko.
- blizu - daleko
- ispred - iza
- ispod - iznad
- lijevo - desno
- vodoravno - uspravno.
- kugla
- kvadar
- kocka
- valjak
- stožac
- piramida.
Navoditi učenike na pravilno izgovaranje i imenovanje navedenih ključnih pojmova.
U okviru ove tematske cjeline poticati razvijanje vještine uspoređivanja i procjenjivanja prema određenom kriteriju.
Uspoređivati po zadanom kriteriju i potkrijepiti učenicima bliskim primjerima (npr. dulji i kraći red u čekaonici, više i niže ljestve, uže i šire hlače).
Sadržaje ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Likovna kultura (crtanje predmeta po boji, visini, širini) i Priroda i društvo (orijentacija u prostoru).
Tražiti od učenika da odrede tko sjedi blizu, a tko daleko, tko ispred ili iza, tko lijevo ili desno u odnosu na njih te što će se dogoditi kad netko od učenika ili on sam promijeni položaj.
Na predmetima u učionici i u neposrednom okruženju pokazati i demonstrirati koji predmeti leže vodoravno, a koji stoje uspravno.
Kod pojašnjavanja pojmova vodoravno i uspravno kao primjer koristiti retke u bilježnici, retke i stupce u križaljci i tablici i sl.
Sadržaje ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Likovna kultura (prostorno oblikovanje) i Tjelesna i zdravstvena kultura (igre dodavanja loptom, blizu - daleko, ispod - iznad).
Upoznavati učenike s predmetima navedenih oblika. Učenici će se s predmetima oblika kocke, kugle, kvadra, valjka, stošca i piramide upoznavati na konkretnim modelima uzimajući ih u ruke, okrećući ih, razgledavajući ih, a potom i imenujući ih. Iz skupa modela izdvajati prvo kugle, kocke i kvadre, a zatim stošce, piramide i valjke. Bitno je prepoznavati oblike u različitim orijentacijama i veličinama.
Povezivati geometrijska tijela s predmetima iz okoline koja ih okužuje (škola, ormar, spužva, lopta, globus i slično) služeći se uzorcima ili vjernim ilustracijama
Sadržaj ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Hrvatski jezik (pisanje naziva geometrijskih tijela) i Likovna kultura (masa i prostor).
C.I.4 Učenik razlikuje likove oblika kruga, trokuta, pravokutnika i kvadrata.
C.I.5 Učenik prikazuje točku kao sjecište crta.
MTP-3.1.2 MTP-3.1.1 - navodi sličnosti i razlike zadanih likova
- imenuje zadane likove
- zadane likove crta uz pomoć šablona ili zadanih predložaka
- prepoznaje ravne i zakrivljene crte kojima su likovi omeđeni
- likove prepoznaje kao strane geometrijskih tijela.
- imenuje ravne i zakrivljene crte
- crta ravne i zakrivljene crte
- označava točku kao sjecište crta
- identificira razliku između otvorene i zatvorene crte
- navodi što je unutar, što na, a što izvan zatvorene crte.
- krug
- trokut
- pravokutnik
- kvadrat.
- crta
- točka
- unutar, na, izvan.
Skicirane likove učenici izrezuju i od njih slažu različite oblike (kamion, ptica, robot, bor..).
Na putu od kuće do škole učenik promatra prometne znakove navedenih oblika.
Kredom, na školskom igralištu, učenici crtaju različite oblike (likove) i kreću se po njima na različite načine.
Sadržaje ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Priroda i društvo (prometni znakovi), Likovna kultura (crtanje oblika iz okruženja).
Učenici u bilježnici i na ploči crtaju različite crte. Opisuju ih i navode sličnosti i razlike među njima. Ne koriste ravnalo.
Od točke A do točke B učenici hodaju po učionici opisujući svoju putanju i birajući najkraći put.
Unutar i izvan zatvorenih crta crtamo predmete ili sl, te navodimo gdje se što nalazi.
Analiziramo može li se nešto nalaziti istovremeno i unutar, i izvan i na. (Knjiga je na stolu, ali je izvan ormara, unutar učionice).
Sadržaj ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Priroda i društvo (put od kuće do škole) i Likovna kultura (crte po toku i karakteru).
- Osnovno
- II
Godine učenja i podučavanja predmeta: 2 A Skupovi, brojevi i operacije A.II.1
A.II.2C Geometrija i mjerenja C.II.1
C.II.2
C.II.3
C.II.4
C.II.5D Podaci, statistika i vjerojatnost D.II.1 A
Skupovi, brojevi i operacijeA.II.1 Učenik primjenjuje zbrajanje i oduzimanje prirodnih brojeva do 20 pri rješavanju tekstualnih zadataka.
A.II.2 Učenik se koristi prirodnim brojevima do 20 u određivanju redoslijeda i količine.
MTP-1.2.1 MTP-1.1.2 - zbraja i oduzima brojeve do 20
- rješava brojevne izraze koji uključuju brojeve do 20 koristeći zamjenu mjesta pribrojnicima
- primjenjuje računske operacije zbrajanja i oduzimanja brojeva do 20 za rješavanje tekstualnih zadataka u različitim kontekstima
- određuje nepoznati član zbroja i razlike koristeći veze zbrajanja i oduzimanja.
- broji, zapisuje i čita brojeve do 20 brojkom i brojevnom riječju
- uspoređuje brojeve do 20
- prikazuje brojeve do 20 na brojevnoj crti
- dodaje i oduzima broj 1
- određuje prethodnik i sljedbenik broja
- razlikuje jednoznamenkaste i dvoznamenkaste brojeve
- formira nizove brojeva do 20
- razlikuje glavne i redne brojeve do 20
- određuje parne i neparne brojeve do 20.
- plus (+), minus (-), jednako (=)
- zbroj i razlika
- zbrajanje i oduzimanje brojeva do 20
- zamjena mjesta pribrojnicima
- veza zbrajanja i oduzimanja.
- brojevi od 1 do 20
- prethodnik i sljedbenik
- uspoređivanje brojeva do 20 i znakovi <, >, =
- brojevna crta i brojevni niz
- redni i glavni brojevi
- parni i neparni brojevi.
Zbrajanje i oduzimanje brojeva do 5 započinje konkretnim primjerima iz okoline ili didaktičkim ilustracijama, pitanjima: „Za koliko je više?“, tj. „Za koliko je manje?“, kad je riječ o oduzimanju. Prije nego se prijeđe na matematički zapis može se upotrijebiti brojevna crta za zbrajanje i oduzimanje (na primjer: Za koliko je broj 5 veći od broja 2? Stavi se olovka na broj 2 i gleda se koliko je 2 „udaljen“ od 5).
Uvode se znakovi: + (plus), – (minus) i = (jednako). Važno je osvješćivati znak = koji prikazuje jednakost lijeve i desne strane. Učenike poticati da za provjeru koriste suprotnu operaciju, što znači ako je učenik morao zbrojiti – oduzimanjem provjerava.
Poželjno je raditi s učenicima zadatke oblika 2+□=5, gdje će se primjenom suprotne računske operacije doći do broja koji treba upisati u kvadratić.
Kroz zadatke učenici uočavaju svojstvo komutativnosti i asocijativnosti iako te pojmove ne koriste.
Postupno proširujemo skup prirodnih brojeva, prvo do 10, a potom do 20, korištenjem istih ili sličnih aktivnosti.
Sadržaj ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Priroda i društvo (problemski zadaci povezani sa sadržajima iz Prirode i društva) i Hrvatski jezik (razumijevanje pročitanog).
Učenici su već upoznati s brojevima od 1 do 10, ali je korisno te brojeve ponoviti i to postupno.
Potrebno je krenuti do broja 5, apstraktnim brojanjem, zapisivanjem, a potom brojanjem i praktičnim aktivnostima. Učenici mogu izrađivati brojeve od plastelina, kamenčića ili grančica, a ne samo biti ograničeni na slikovne brojke jer je za učenike to previše apstraktno.
Kroz igru Pogodi koliko ima? dodavanjem predmeta ili objekta učenici osvješćuju da svaki sljedeći broj nastaje dodavanjem broja 1 prethodnomu broju. Samim tim usvajaju pojmove prethodnik i sljedbenik nekog broja, a zatim te brojeve mogu stavljati na već pripremljenu brojevnu crtu (broj neposredno ispred i neposredno iza). Tako se stvara jasna poveznica među naučenim pojmovima.
Postupno se spoznaje brojenje unaprijed i unatrag (redom i od zadanoga broja) te brojenje zadanim korakom počevši po 2 (po 2 : 2, 4,…) i od zadanoga broja, (od broja 3 broje po 2 : 3, 5,…).
Postupno proširujemo skup prirodnih brojeva, prvo do 10, a potom do 20, korištenjem istih ili sličnih aktivnosti.Pitanjima poput: „Tko sjedi u prvoj klupi?“, „Kako se zove sestra učenici u trećoj klupi?“, „Tko je peti u imeniku?“, učenici razlikuju redne i glavne brojeve te je bitno da razumiju kad ih treba upotrijebiti.
Sadržaj ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Likovna kultura (modeliranje), Engleski jezik (brojevi do 10).
C
Geometrija i mjerenjaC.II.1 Učenik povezuje odnose među predmetima.
C.II.2 Učenik koristi pojmove lijevo - desno, gore - dolje, naprijed - natrag pri kretanju.
C.II.3 Učenik identificira geometrijska tijela i njihove elemente.
MTP-3.1.1 MTP-3.1.3 MTP-3.1.2 - ilustrira svojstvo i položaj jednog predmeta u odnosu na drugi
- izdvaja predmete prema zadanom kriteriju
- slaže predmete i bića prema zadanom kriteriju.
- pokazuje predmete koji se nalaze lijevo - desno, gore - dolje, naprijed - natrag u odnosu na sebe i na zadani orijentir
- smješta predmete i bića u zadani položaj
- određuje smjer i pravac kretanja promatranih bića i predmeta.
- imenuje kuglu, valjak, kvadar, piramidu i stožac
- prepoznaje sličnost geometrijskih tijela s predmetima u okruženju, na modelima geometrijskih tijela i na ilustracijama
- razlikuje zakrivljene plohe od ravnih
- imenuje ravne plohe geometrijskih tijela kao geometrijske likove
- prepoznaje i imenuje bridove i vrhove na modelima geometrijskih tijela.
- viši - niži
- dulji - kraći
- širi - uži
- veći - manji - jednak
- unutar - izvan - na.
- lijevo - desno
- gore - dolje
- naprijed - natrag
- u sredini
- između.
- geometrijska tijela; kugla, valjak, kvadar, kocka, piramida
- geometrijski likovi; krug, pravokutnik, kvadrat trokut
- ravna i zakrivljena ploha
- bridovi
- vrhovi.
Uz učenicima prilagođene primjere i njima bliske predmete i bića, pojasniti razlike među navedenim ključnim pojmovima.
Učenik bi trebao usporediti i pravilno imenovati odnose među predmetima, npr. nacrtano je stablo, učeniku se može zadati da nacrta niže stablo i sl. Pozornost treba biti usmjerena na pravilnom odabiru riječi suprotnog značenja.
Na crtežu kuće učeniku se može zadati da nacrta loptu ispred kuće, iznad kuće sunce, desno od kuće cvijet i sl.
Sadržaj ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Likovna kultura (crtanje) i Hrvatski jezik (riječi suprotnog značenja).
Učenici kroz igru vježbaju načine kretanja prema zadanim uputama (npr. učenik se s povezom preko očiju treba kretati učionicom od točke A do točke B slijedeći upute koje mu daju drugi učenici).
Učenici navode predmete koji se nalaze između dva zadana objekta.
Učenici u zadanom vremenu prate kretanje bića i vozila u svojem vidokrugu te međusobno uspoređuju zapažanja.
Sadržaj ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Priroda i društvo (problemski zadaci povezani sa sadržajima iz Prirode i društva) i Tjelesna i zdravstvena kultura.
Nakon što su učenici upoznati s geometrijskim tijelima, skiciraju/crtaju likove i predmete oblika geometrijskih tijela. Učenici na skicama predmeta geometrijskih tijela pronalaze ravne i zakrivljene plohe.
Geometrijske likove učenici upoznaju kao ravne plohe geometrijskih tijela. Tako se stvara jasna poveznica među geometrijskim objektima.
Primjer: dvoje djece sjedi jedno nasuprot drugom, između je pregrada da se ne vidi što se događa na drugoj strani. Jedan učenik od modela za slaganje u obliku geometrijskih tijela napravi figuru. Zatim drugom učeniku daje precizne upute za izradu jednake figure. Kada se pregrada ukloni, figure moraju biti jednake.
Učenici na vjerodostojnim skicama geometrijskih tijela zaokružuju točke koje imenuju vrhovima kocke, kvadra i piramide. Spajanjem točaka identificiraju bridove.
Sadržaj ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Likovna kultura (crtanje, modeliranje), Priroda i društvo (problemski zadaci povezani sa sadržajima iz Prirode i društva) i Hrvatski jezik (usmeno i pismeno izražavanje).
C.II.4 Učenik crta izlomljene, zatvorene i otvorene crte, te crte koje se sijeku.
C.II.5 Učenik se koristi valutama za novac u skupu brojeva do 20 pri rješavanju problemskih zadataka u različitim kontekstima.
MTP-3.1.1 MTP-3.2.1 - povezuje dvije točke ravnom ili zakrivljenom crtom
- crta izlomljene, zatvorene i otvorene crte
- crta crte koje se sijeku uočavajući njihovo sjecište
- koristi ravnalo pri crtanju ravnih crta.
- imenuje mjerne jedinice za novac i njihove vrijednosti
- uspoređuje vrijednosti kovanica i novčanica
- računa s novcem u skupu brojeva do 20
- koristi novčane vrijednosti u skupu do 20 pri rješavanju problemskih zadataka u različitim kontekstima.
- ravna i zakrivljena crta
- izlomljena, otvorena i zatvorena crta
- točka
- sjecište crta.
- novac
- novčana valuta (konvertibilna marka, fening).
Uz različite didaktičke igre s konopcem ili s vunicom omogućiti učenicima da ravnu crtu dožive kao najkraći put između dvije točke, a zakrivljenu crtu kao dulji put.
Označiti dvije točke na ploči i pitati ih s koliko ravnih crta mogu spojiti navedene točke. Isto napraviti i sa zakrivljenim crtama.
Pokazati da se dvije ravne crte mogu sjeći samo u jednoj točki, a dvije zakrivljene kao i jedna ravna i jedna zakrivljena u više točaka.
Navesti učenike da kroz jednu točku povuku nekoliko crta, bilo ravnih ili zakrivljenih i da zaključe mogu li ih nacrtati još.
Napisati riječ na ploču, npr. M A T E M A T I K A i pitati ih, kakvim smo crtama napisali zadanu riječ. Isto učiniti s riječi koja ima slova sa zakrivljenim crtama, npr. P L O Č A.
Sadržaj ove tematske cjeline može se povezati sa sadržajem nastavnog predmeta Likovna kultura (crtanje).
Pri učenju prepoznavanja novčanica i kovanica najvažnije za učenike je da osvijeste važnost primjene računanja izvan školskih klupa, a to se može postići kroz rješavanje problemskih zadataka u različitim kontekstima u kojima se koristi novac.
Može se odglumiti neki događaj iz stvarnog života u kojem učenici trebaju koristiti zbrajanje i oduzimanje (npr. odlazak u kupnju, raspodjelu novca i sl.). Poželjno je potaknuti učenika da samostalno štede novac te tako razvijaju poduzetničke vještine.
Sadržaj ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Hrvatski jezik (usmeno izražavanje), Priroda i društvo (problemski zadaci povezane sa sadržajima iz Prirode i društva) te međupredmetnim temama Poduzetnost (novac, štednja) i Građanski odgoj i obrazovanje (odgovornost).
D
Podaci, statistika i vjerojatnostD.II.1 Učenik čita podatke i prikazuje ih piktogramima i tablicama.
MTP-4.1.1 - čita podatke iz piktograma i tablica
- raspoređuje podatke u piktograme i tablice.
- podatci
- piktogram
- tablica
- stupac i redak.
Učenici se prvi put susreću s podatcima stoga je poželjno koristiti samo jednostavne primjere, tj. podatke iz neposredne učenikove okoline.
U početku učenici te podatke slikovno (količinski) uspoređuju na crtežima, u skupovima ili piktogramima, a kasnije i brojčano u tablicama radi donošenja jednostavnih i učenicima bliskih zaključaka.
Uz podatke učenici upoznaju različite načine prikupljanja, uređivanja i prezentiranja podataka na primjerima iz svakodnevnog života. U tabličnim prikazima važno je ispravno se koristiti izrazima redak i stupac.
Sadržaj ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Priroda i društvo (problemski zadaci povezane sa sadržajima iz Prirode i društva), Likovna kultura (crtanje) i s međupredmetnim temama Učiti kako učiti i Poduzetnost (osobne potrebe).
- Osnovno
- III
Godine učenja i podučavanja predmeta: 3 A Skupovi, brojevi i operacije A.III.1
A.III.2
A.III.3
A.III.4
A.III.5C Geometrija i mjerenja C.III.1
C.III.2D Podaci, statistika i vjerojatnost D.III.1
D.III.2A
Skupovi, brojevi i operacijeA.III.1 Učenik se koristi prirodnim brojevima do 100 pri određivanju redoslijeda i količine.
A.III.2 Učenik zapisuje i čita rimske brojeve do 12.
A.III.3 Učenik primjenjuje zbrajanje i oduzimanje prirodnih brojeva do 100 pri rješavanju problemskih zadataka u različitim kontekstima.
MTP-1.1.1 MTP-1.1.2 MTP-1.2.1 - broji, zapisuje i čita prirodne brojeve do 100 brojkom i brojevnom riječju
- razlikuje odnose među dekadskim jedinicama (jedinice, desetice i stotice)
- određuje mjesnu vrijednost pojedine znamenke
- određuje prethodnik i sljedbenik zadanog broja
- formira i nastavlja nizove brojeva
- uspoređuje brojeve do 100 i koristi znakove <, >, =
- prikazuje brojeve do 100 na brojevnoj crti
- razlikuje glavne i redne brojeve do 100.
- nabraja osnovne i pomoćne rimske znamenke
- čita i zapisuje brojeve do 12 rimskim znamenkama.
- zbraja i oduzima u skupu prirodnih brojeva do 100
- računa vrijednost brojevnih izraza koji uključuju prirodne brojeve do 100 koristeći zamjenu mjesta pribrojnicima
- primjenjuje vezu zbrajanja i oduzimanja
- primjenjuje računske operacije zbrajanja i oduzimanja u skupu prirodnih brojeva do 100 za rješavanje problemskih zadataka u različitim kontekstima.
- skup prirodnih brojeva do 100
- tablica mjesnih vrijednosti
- brojevna crta
- uspoređivanje brojeva do 100 i znakovi <, >, =
- prethodnik i sljedbenik
- glavni i redni brojevi do 100.
- rimske brojke do 12
- brojka, znamenka.
- zbrajanje i oduzimanje
- pribrojnici i zbroj
- umanjenik, umanjitelj i razlika
- zbrajanje i oduzimanje desetica
- zbrajanje dvoznamenkastih i jednoznamenkastih brojeva
- zbrajanje i oduzimanje triju i više brojeva
- uporaba zagrada
- zbrajanje i oduzimanje dvoznamenkastih brojeva do 100
- zamjena mjesta pribrojnicima
- veza između zbrajanja i oduzimanja.
Na konkretnim materijalima (npr. didaktičke ilustracije) usvojiti: postupak brojenja, pravilno čitanje, pisanje brojkom i brojevnom riječju, uspoređivanje i prikazivanje brojeva do 100.
Razlikovati i pravilno zapisivati glavne i redne brojeve.
Pri uspoređivanju prikazati odnose među brojevima i na brojevnoj crti.
Povezati brojevnu riječ, zapis broja i njegov rastav na desetice i jedinice, npr. 73 (sedamdeset tri) = 7 desetica i 3 jedinice.
Prikazati odnos stotice i 10 desetica, odnosno 100 jedinica.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Hrvatski jezik (čitanje s razumijevanjem, pisanje brojevne riječi), Tjelesna i zdravstvena kultura (antropometrijska mjerenja) i Priroda i društvo (Upoznaj svoje mjesto-kućni brojevi).
U neposrednom okruženju uočiti rimske brojeve, npr. sat i kalendar.
Upoznati učenika s povijesnim razvojem arapskih i rimskih znamenaka.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Hrvatski jezik i Priroda i društvo (Snalazimo se u vremenu).
Učenici su postupak zbrajanja i oduzimanja već usvojili u drugom razredu u skupu prirodnih brojeva do 20. Na ovom mjestu je korisno taj postupak ponoviti i nadograditi, najprije zadacima koji uključuju zbrajanje ili oduzimanje bez prijelaza, a zatim zadacima s prijelazom.
Kako bi učenici lakše usvojili pojam destica i jedinica moguće je zadati projektni zadatak u kojem će sami izraditi kartice desetica i jedinica u različitoj boji te ih koristiti za prikaz brojeva do 100, njihovog zbrajanja i oduzimanja (bez prijelaza). Kako bi učenici usvojili zbrajanje i oduzimanje u skupu prirodnih brojeva do 100 prijedlog je igrati igru "Trgovina". Nakon što učenici usvoje pojmove i postupke na zornim primjerima, potaknuti ih na apstraktan pristup i matematički zapis.
Zakoni komutativnosti i asocijativnosti se primjenjuju, ali se ne imenuju.
Pri izvođenju računskih operacija tražiti od učenika pravilno korištenje matematičkih termina: pribrojnik, zbroj, umanjenik, umanjitelj i razlika.
Korisno je da učenici jednostavne primjere iz svakodnevnog života modeliraju brojevnim izrazom uz korištenje pravilnog matematičkog zapisa.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Hrvatski jezik, Priroda i društvo (Rad u trgovini) i s međupredmetnom temom Poduzetnost (osobne potrebe, kupac, dobavljač, robna i novčana razmjena).
A.III.4 Učenik množi i dijeli u skupu brojeva do 100.
A.III.5 Učenik rješava zadatke s više računskih operacija u skupu prirodnih brojeva do 100 poštujući redoslijed računskih operacija.
MTP-1.2.1 MTP-1.2.1 - množi dva broja koristeći uzastopno zbrajanje jednog od njih
- dijeli dva broja koristeći uzastopno oduzimanje djelitelja od djeljenika
- automatizirano množi u skupu prirodnih brojeva do 100 uključujući množenje broja nula
- primjenjuje vezu množenja i dijeljenja.
- izvodi više računskih operacija poštujući redoslijed njihovog izvođenja
- prikazuje matematičkim zapisom brojevni izraz iskazan riječima.
- množenje i dijeljenje do 100
- višekratnici brojeva
- imenovanje članova (faktori, umnožak)
- imenovanje članova (djeljenik, djeljitelj, količnik)
- tablica množenja
- zamjena mjesta faktorima
- veza množenja i dijeljenja.
- redoslijed izvođenja računskih operacija
- redoslijed izvođenja računskih operacija u zadacima sa zagradama.
Množenje i dijeljenje uvesti postupno, a pri tome se oslanjati na zbrajanje i oduzimanje dok učenike ne dovedemo do automatizma.
Isticati vezu između množenja i dijeljenja postavljanjem pitanja poput: "Koliko puta 6 stane u 30? "
Pri izvođenju računskih operacija tražiti od učenika pravilno korištenje matematičkih termina faktori (čimbenici), umnožak (produkt), djeljenik, djelitelj i količnik. Vježbati zadatke u kojima učenik određuje višekratnike zadanog broja (dvokratnik, trokratnik, četverokratnik...) te polovinu, trećinu, četvrtinu,... zadanog broja.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Hrvatski jezik, Priroda i društvo (kućni brojevi-parni i neparni brojevi) i s međupredmetnom temom Građanski odgoj i obrazovanje (pravda, pravilna podjela).
Rješavati zadatke kao što su 8·3-9=, 42:7+3·9=, 50+24:8= i sl. te upozoravati kako se najprije množi, odnosno dijeli, zatim zbraja i oduzima. Učenici trebaju izricati redoslijed izvođenja računskih operacija na osnovi promatranja napisanog zadatka. Zatim prelazimo na zadatke u kojima učenici ovladavaju postupkom računanja s više računskih operacija uz uporabu zagrada. Učenici se trebaju osamostaljivati u postavljanju i rješavanju brojevnih izraza s više računskih operacija.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Hrvatski jezik.
C
Geometrija i mjerenjaC.III.1 Učenik crta dužine i uočava ih na geometrijskim likovima i tijelima.
C.III.2 Učenik koristi mjerne jedinice za duljinu, novac i vrijeme.
MTP-3.1.1 MTP-3.2.1 - crta i opisuje dužinu
- određuje pripadnost točaka dužini
- određuje vrhove geometrijskih tijela i likova kao točke
- određuje stranice geometrijskih likova i bridove geometrijskih tijela kao dužine.
- mjeri duljine standardnim mjernim jedinicama za duljinu
- iskazuje vrijeme standardnim mjernim jedinicama za vrijeme
- računa s istim mjernim jedinicama za duljinu, vrijeme i novac.
- dužina
- dužina i točke na likovima
- dužina i točke na tijelima.
- mjerenje duljine dužine
- jedinice za duljinu (milimetar, centimetar, decimetar, metar, kilometar).
- jedinice za vrijeme (sekunda, minuta, sat, dan, tjedan, mjesec, godina).
- jedinice za novac u Bosni i Hercegovini i Republici Hrvatskoj.
Ponoviti znanja o crti i točki. Na ploči nacrtati dvije točke A i B koje će učenici spajati različitim crtama (ravnom, zakrivljenom i izlomljenom). Promatrajući crtež učenici će uočiti koja je crta najkraća. Objasniti učenicima da je najkraća spojnica dviju točaka dužina, koje su njene krajnje točke npr. A i B te kako se dužina označava. Na crtežima geometrijskih tijela i likova uočiti vrhove, bridove i stranice geometrijskih likova.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Hrvatski jezik, Tjelesna i zdravstvena kultura i Likovna kultura.
Učenici mjere duljinu na različite načine: stopalom, korakom, spajalicom, olovkom, gumicom,... Zadati učenicima neka izmjere duljinu olovke ravnalom. Objašnjavamo im da je razmak između dvaju brojeva na ravnalu označava centimetre.
S učenicima je poželjno osmisliti aktivnosti pomoću kojih će lakše prepoznavati novčanice i kovanice. To se može postići kroz zadatke riječima u kojima se koristi novac. Također, učenici mogu pomoću igre "Trgovina" vježbati zbrajanje i oduzimanje do 100. Razvijati kod učenika kritičko razmišljanje o potrošnji.
Učenici određuju vremenske intervale u svakodnevnim situacijama. Uvodimo mjerne jedinice za vrijeme: sat, minuta, sekunda, dan, tjedan, mjesec i godina, te računamo s njima u skupu prirodnih brojeva do 100.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Hrvatski jezik i Priroda i društvo.
D
Podaci, statistika i vjerojatnostD.III.1 Učenik prikazuje i interpretira podatke prikazane piktogramima i tablicama.
D.III.2 Učenik određuje je li neki događaj moguć ili nemoguć.
MTP-4.1.1 MTP-4.2.2 - prikuplja i razvrstava podatke iz svakodnevnog života
- prikazuje podatke jednostavnim tablicama i piktogramima
- objašnjava podatke prikazane jednostavnim tablicama i piktogramima.
- razlikuje je li neki događaj moguć ili nemoguć
- objašnjava je li neki događaj (ne)moguć.
- tablica
- piktogram.
- događaj
- moguć ili nemoguć događaj.
Vježbati s učenicima čitanje raznih prikaza podataka uz objašnjenje zaključaka.
Učenici će dobiti gotove tablice u kojima će prikazivati podatke razrednog istraživanja. Razredno istraživanje može biti povezano npr. s nastavnim predmetom Priroda i društvo. Učenici će bilježiti broj sunčanih/kišnih dana.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Hrvatski jezik, Priroda i društvo i Tjelesna i zdravstvena kultura .
Kroz razgovor s učenicima uvesti pojam vjerojatnosti. Npr. postavljati im pitanja tipa:
Je li moguće da ćete na satu matematike igrati nogomet?
Je li moguće da ćete na poklon za rođendan dobiti loptu?
Je li moguće da pri bacanju dviju igraćih kocki ukupan zbroj bude 15?
Je li moguće da pri bacanju dviju igraćih kocki ukupan zbroj bude manji od 10?
Ako u posudi imamo 5 crvenih i 5 plavih loptica, je li moguće da ćeš izvući zelenu lopticu?
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Hrvatski jezik.
- Osnovno
- IV
Godine učenja i podučavanja predmeta: 4 A Skupovi, brojevi i operacije A.IV.1
A.IV.2
A.IV.3
A.IV.4
A.IV.5B Algebra B.IV.1
B.IV.2C Geometrija i mjerenja C.IV.1
C.IV.2D Podaci, statistika i vjerojatnost D.IV.1 A
Skupovi, brojevi i operacijeA.IV.1 Učenik se koristi prirodnim brojevima do 1000 pri opisivanju količine i redoslijeda.
A.IV.2 Učenik zapisuje i čita rimske brojeve do 1000.
A.IV.3 Učenik primjenjuje zbrajanje i oduzimanje brojeva do 1000 pri rješavanju problemskih zadataka različitih konteksta.
MTP-1.1.2 MTP-1.1.2 MTP-1.2.1 - broji, čita i zapisuje brojem i brojevnom riječju brojeve do 1000.
- zapisuje brojeve na brojevnoj crti i u tablici mjesnih vrijednosti.
- određuje mjesnu vrijednost pojedine znamenke.
- određuje dekadske jedinice i njihove odnose.
- uspoređuje brojeve do 1000 i koristi znakove <, > i =.
- određuje prethodnik i sljedbenik broja.
- rastavlja broj na zbroj višekratnika dekadskih jedinica.
- nabraja i zapisuje osnovne i pomoćne rimske brojeve.
- čita i zapisuje rimskim znamenkama brojeve do 1000.
- pisano zbraja i oduzima brojeve do 1000, primjenjujući odgovarajući matematički zapis.
- računa vrijednost brojevnih izraza koji uključuju zbrajanje i oduzimanje brojeva do 1000 koristeći zamjenu mjesta pribrojnicima.
- primjenjuje računske operacije zbrajanja i oduzimanja u skupu prirodnih brojeva do 1000 za rješavanje problemskih zadataka različitih konteksta.
- skup prirodnih brojeva do 1000
- tablica mjesnih vrijednosti
- brojevna crta
- uspoređivanje brojeva i znakovi <, > i =
- dekadske jedinice
- prethodnik i sljedbenik
- rastavljanje brojeva na zbroj višekratnika dekadskih jedinica
- rimski brojevi.
- pisano zbrajanje i oduzimanje
- zamjena mjesta pribrojnicima
- problemski zadaci sa zbrajanjem i oduzimanjem različitih konteksta
Pomoću konkretnih didaktičkih materijala učenicima dočarati brojanje, čitanje i pisanje u skupu brojeva do 1000.
Pomoću različitih primjera navoditi učenike da sami uoče pravila za uspoređivanje brojeva.
Koristiti se brojevnom crtom pri određivanju prethodnika i sljedbenika broja.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Hrvatski jezik (brojevna riječ) i Priroda i društvo (desetljeće, stoljeće i tisućljeće).
Učenicima možemo olakšati pisanje rimskim brojevima tako što im objasnimo kako trebaju rastaviti arapski broj na stotice, desetice i jedinice i obrnuto.
Npr. 624 = 500 + 100 + 20 + 4
DCXXIV = D + C + XX + IV
Pisanje i čitanje rimskim znamenkama možemo proširiti i do 2000 ako su učenici bez poteškoća svladali čitanje i pisanje rimskim znamenkama do 1000.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Priroda i društvo (desetljeće, stoljeće i tisućljeće).
Postupak pisanog zbrajanja i oduzimanja provodi se postupno, najprije se pisano zbrajaju i oduzimaju brojevi do 100, a nakon toga brojevi do 1000.
Pri pisanom oduzimanju prednost dati tzv. aditivnom načinu oduzimanja (5 do 8 je 3, 7 do 13 je 6) što će omogućiti povezivanje dviju računskih operacija u jednu spoznajnu cjelinu.
Poželjno bi bilo upotpuniti nastavu Matematike zadacima iz svakodnevnog života u kojima će učenici uz primjenu stečenih znanja iz Matematike razvijati sposobnost kritičkog mišljenja i zaključivanja.
Zakoni komutativnosti i asocijativnosti se primjenjuju, ali se ne imenuju.
Češće poticati učenike na imenovanje članova računskih operacija.
A.IV.4 Učenik pisano množi i dijeli jednoznamenkastim brojem u skupu prirodnih brojeva do 1000.
A.IV.5 Učenik računa vrijednost brojevnog izraza s više računskih operacija u skupu prirodnih brojeva do 1000, sa zagradama.
MTP-1.2.1 MTP-1.2.1 - množi i dijeli s 10, 100 i 1000.
- pisano množi jednoznamenkastim brojem u skupu prirodnih brojeva do 1000.
- pisano dijeli jednoznamenkastim brojem u skupu prirodnih brojeva do 1000 na duži i kraći način.
- dijeli jednoznamenkastim brojem u skupu prirodnih brojeva do 1000 s ostatkom.
- provjerava rješenje pri dijeljenju s ostatkom.
- primjenjuje vezu množenja i dijeljenja.
- računa vrijednost brojevnih izraza s više računskih operacija i zagrada poštujući redoslijed računskih operacija.
- brojevni izraz iskazan riječima prikazuje matematičkim zapisom s više računskih operacija i zagrada.
- pisano množenje i dijeljenje
- dijeljenje s ostatkom
- članovi računskih operacija (faktori, umnožak, djeljenik, djelitelj, količnik)
- veza množenja i dijeljenja.
- brojevni izraz
- redoslijed izvođenja računskih operacija
- zadaci sa zagradama
- zadaci s više računskih operacija.
Češće uvježbavati i povezivati množenje i dijeljenje kako bi se potaklo učenike na samostalno provjeravanje točnosti rješenja.
Češće zadavati zadatke zadane riječima u kojima učenici trebaju samostalno donositi zaključke o tome kojom će se računskom radnjom koristiti kako bi došli do točnog rješenja.
Preporuča se zadavati što više primjera u kojima učenici trebaju sami postaviti brojevni izraz, npr. trokratnik broja 198 umanji za razliku brojeva 913 i 682.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Hrvatski jezik (redoslijed događaja).
B
AlgebraB.IV.1 Učenik rješava problemske zadatke različitih konteksta odabirom odgovarajućeg matematičkog postupka u skupu prirodnih brojeva do 1000.
B.IV.2 Učenik određuje vrijednost nepoznatog člana jednakosti koristeći slovo kao zamjenu za broj.
MTP-2.2.1 MTP-2.2.1 - uočava poznate i nepoznate podatke problemskog zadatka različitog konteksta.
- postavlja odgovarajući brojevni izraz na temelju problemskog zadatka različitog konteksta.
- rješava problemske zadatke različitih konteksta.
- koristi slovo kao zamjenu za broj.
- opisuje postupak kojim će odrediti nepoznati član jednakosti.
- određuje vrijednost nepoznatog člana jednakosti.
- primjenjuje veze među računskim operacijama.
- utvrđuje ispravnost matematičkog postupka i smislenost dobivenog rješenja.
- problemski zadaci različitih konteksta
- matematički postupci.
- nepoznati član
- jednakost
- veze među računskim operacijama
- provjera ispravnosti matematičkog postupka.
Učenike usmjeravati na pažljivo promišljanje pri postavljanju i rješavanju problemskih zadataka različitih konteksta na način da uoče poznate podatke i jasno izraze ono što je u zadatku potrebno odrediti.
Sadržaje ove tematske jedinice moguće je korelirati sa sadržajima nastavnog predmeta Hrvatski jezik (jezično izražavanje).
Pri postupku izračunavanja nepoznatog člana jednakosti, preporučuje se poticati učenike na opisivanje postupka kojim će izračunati nepoznati član jednakosti.
Npr. u jednakosti x - 123 = 321, nepoznati umanjenik izračunavamo tako što razliku i umanjitelj zbrojimo.
Važno je poticati učenike na utvrđivanje smislenosti rezultata i provjeru ispravnosti matematičkog postupka.
C
Geometrija i mjerenjaC.IV.1 Učenik određuje odnos između različitih skupova točaka u ravnini.
C.IV.2 Učenik određuje mjerljiva obilježja geometrijskih likova i tijela.
MTP-3.1.1 MTP-3.2.1 - opisuje ravninu i određuje pripadnost ravnini.
- prepoznaje, opisuje i crta pravce, polupravce i dužine kao dijelove pravca te njihove odnose.
- određuje pripadnost točaka pravcu, polupravcu i dužini.
- koristi matematičke oznake za dužinu, pravac i polupravac, te usporednost i okomitost pravaca.
- crta dužinu zadane duljine
- zapisuje duljinu dužine odgovarajućim matematičkim znakovima
- imenuje mjerne jedinice za duljinu i masu, kao i mjerne jedinice za volumen (tekućine)
- procjenjuje i mjeri duljinu i masu, kao i volumen (tekućine), odgovarajućim mjernim instrumentom
- računa s mjernim jedinicama za duljinu i masu, kao i s mjernim jedinicama za volumen (tekućine)
- preračunava mjerne jedinice za duljinu i masu, kao i one za volumen (tekućine), iz većih u manje i obrnuto
- opisuje opseg kao zbroj duljina stranica geometrijskog lika (trokuta, pravokutnika i kvadrata)
- izračunava opseg trokuta, pravokutnika i kvadrata.
- ravnina
- pravac
- polupravac
- dužina
- sjecište pravaca
- pravci koji se sijeku
- usporedni i okomiti pravci
- pripadnost točke dužini, pravcu i polupravcu
- matematičke oznake za dužinu, pravac i polupravac, te usporednost i okomitost pravaca.
- duljina
- jedinice za duljinu (kilometar, metar, decimetar, centimetar i milimetar)
- volumen tekućine
- jedinice za volumen tekućine (litar, decilitar i mililitar)
- masa
- jedinice za masu (tona, kilogram, dekagram i gram)
- mjerni instrumenti (ravnalo, posude za tekućinu, vaga)
- preračunavanje mjernih jedinica
- opseg
- opseg trokuta
- opseg pravokutnika
- opseg kvadrata.
Izraditi dodatne didaktičke materijale kao npr. plakat s prikazom geometrijskih likova u ravnini.
Usporedne i okomite pravce prepoznavati na različitim likovima i predmetima koji se svakodnevno upotrebljavaju.
Pomoću kvadratne mreže uvježbati okomite i usporedne pravce.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Likovna kultura (crte po toku i karakteru) i Priroda i društvo (plan mjesta).
Učenicima približiti mjerne jedinice za mjerenje duljine i mase kroz igru u kojoj će mjeriti duljinu i masu njima bliskih predmeta ili dijelova tijela npr. duljinu podlaktice, nadlaktice, stopala itd.
Preporučuje se uvesti mjerenje uz pomoć improviziranog ravnala koje ne počinje mjeriti od 0 cm, već nekim dugim brojem npr. 4.
U izračunavanju opsega, osim ravnalom, učenici se mogu služiti i špagom ili koncem.
Naglašavati izražavanje veličine opsega odgovarajućom mjernom jedinicom.
Sadržaje ove tematske jedinice moguće je korelirati sa sadržajima nastavnih predmeta: Tjelesna i zdravstvena kultura (mjerenja) i Hrvatski jezik (kratice).
D
Podaci, statistika i vjerojatnostD.IV.1 Učenik koristi tablice i stupčaste dijagrame za prikaz podataka.
MTP-4.1.1 - identificira stupac, redak i polje
- prikazuje podatke tablicama i stupčastim dijagramima
- čita podatke iz tablica i stupčastih dijagrama.
- stupac
- redak
- polje
- tablice
- podaci
- stupčasti dijagram.
Učenici trebaju uz pojmove stupac, redak i polje usvojiti i pojam ćelije kao sinonim za polje.
Kroz projektni zadatak učenici mogu npr. napraviti istraživanje "Kućni ljubimci u mom razredu". Podijeljeni u heterogene parove rješavaju zadatak, a na idućem satu izlažu dobivena rješenja te uspoređuju s ostalim parovima u razredu.
a) Koji je kućni ljubimac najdraži učenicima tvog razreda?
b) Koliko učenika u razredu ima kućnog ljubimca?
c) Koliko učenika u razredu nema kućnog ljubimca?
d) Prikaži podatke u tablici.
e) Prikaži podatke stupčastim dijagramom.
Poželjno je prikazivati podatke služeći se primjerenom tehnologijom.
Preporučuje se korištenje grafičkih prikaza i u drugim predmetima.
Sadržaje ove tematske cjeline moguće je korelirati sa svim nastavnim predmetima.
- Osnovno
- V
Godine učenja i podučavanja predmeta: 5 A Skupovi, brojevi i operacije A.V.1
A.V.2
A.V.3B Algebra B.V.1
B.V.2C Geometrija i mjerenja C.V.1
C.V.2
C.V.3
C.V.4
C.V.5D Podaci, statistika i vjerojatnost D.V.1
D.V.2A
Skupovi, brojevi i operacijeA.V.1 Učenik koristi brojeve do milijun pri opisivanju količine i redoslijeda.
A.V.2 Učenik primjenjuje pisano zbrajanje i oduzimanje brojeva do milijun pri rješavanju problemskih zadataka različitih konteksta.
A.V.3 Učenik primjenjuje pisano množenje i dijeljenje dvoznamenkastim brojem brojeva do milijun pri rješavanju problemskih zadataka različitih konteksta.
MTP-1.1.1 MTP-1.2.1 MTP-1.2.1 - broji, čita i zapisuje brojeve do milijun
- uspoređuje brojeve do milijun
- prepoznaje mjesne vrijednosti znamenaka.
- pisano zbraja i oduzima u skupu prirodnih brojeva do milijun
- računa vrijednost brojevnih izraza s brojevima do milijun koristeći zamjenu mjesta pribrojnika i združivanje pribrojnika u zagrade
- primjenjuje računske operacije zbrajanja i oduzimanja brojeva do milijun pri rješavanju problemskih zadataka različitih konteksta.
- pisano množi dvoznamenkastim brojem
- pisano dijeli dvoznamenkastim brojem na kraći način
- procjenjuje rezultat tijekom množenja i dijeljenja
- rješava problemske zadatke različitih konteksta primjenjujući vezu između množenja i dijeljenja.
- brojevi do milijun
- višeznamenkasti brojevi
- mjesna vrijednost znamenaka
- uspoređivanje bojeva do milijun.
- pisano zbrajanje i oduzimanje višeznamenkastih brojeva
- zamjena mjesta pribrojnika i združivanje pribrojnika
- veza zbrajanja i oduzimanja.
- pisano množenje dvoznamenkastim brojem
- zamjena mjesta faktorima i združivanje faktora
- pisano dijeljenje dvoznamenkastim brojem
- veza množenja i dijeljenja.
Posebnu pozornost obratiti prilikom brojanja na prijelazima desettisućica i stotisućica (npr. Navedi neposrednog prethodnika broja 1000000).
Sadržaj ove nastavne cjeline može se povezati sa sadržajima nastavnih predmeta: Hrvatski jezik (jezično izražavanje, Brojevi) i Priroda i društvo (broj stanovnika, vremenska lenta).
Iako se izrazi komutativnost i asocijativnost ne koriste, poželjno je raditi zadatke koji zahtijevaju primjenu tih svojstava.
Sadržaj ove nastavne cjeline može se povezati sa sadržajem nastavnog predmeta Priroda i društvo (broj stanovnika zavičaja, reljef) i međupredmetnom temom Poduzetnost.
U pisanom dijeljenju dvoznamenkastim brojevima potrebno je uvježbati i poticati učenike na pravilne procjene količnika tijekom postupka dijeljenja.
Sadržaj ove tematske cjeline može se povezati s međupredmetnim temama Poduzetnost i Građanski odgoj i obrazovanje.
B
AlgebraB.V.1 Učenik primjenjuje odnose među brojevima, svojstva i veze računskih operacija pri određivanju vrijednosti nepoznatog člana u jednakostima i nejednakostima.
B.V.2 Učenik rješava problemske zadatke odabirom odgovarajućeg matematičkog postupka koristeći brojeve do milijun.
MTP-2.2.1 MTP-2.1.1 - primjenjuje odnose među brojevima pri određivanju nepoznatog člana nejednakosti
- određuje vrijednost nepoznatog člana jednakosti koristeći slovo kao oznaku za broj i veze između računskih operacija.
- argumentira izbor računskih operacija i strategije rješavanja zadataka
- rješava problemske zadatke koristeći odnose među brojevima, računske operacije, njihove veze i svojstva te zagrade
- tumači dobiveno rješenje zadanog problema.
- slovo kao oznaka za broj
- jednakost i nejednakost, nepoznanica.
- problemski zadaci.
Polazna točka bi bila usvajanje i razlikovanje pojmova jednakosti i nejednakosti te postupaka određivanja nepoznatog člana. Pri određivanju nepoznatog člana jednakosti koristi se veza računskih operacija i preporučuje obvezna provjera točnosti rješenja.
Primjer: Koji broj treba upisati umjesto slova x tako da jednakost bude točna?
54 663+x= 58 921,
x=58 921-54 663
x=4 258
Provjera: 54 663+4258=58 921
Sadržaj ove tematske cjeline može se povezati s međupredmetnom temom Osobni i socijalni razvoj.
Primarni cilj rješavanja problemskih zadataka je poticati učenike na uočavanje problema, izbor računskih operacija i pravilan izbor strategija kojima će pronaći rješenje.
Postavljeni zadaci mogu sadržavati termine polovina, trećina,...osmina čime bi učenike uvodili u razlomke (ali ne uvoditi zapis razlomka).
Npr. trećinu broja 882 uvećaj za najveći četveroznamenkasti broj.
Učenici bi trebali sami procjenjivati rezultate zadataka, argumentirati postavljeni brojevni izraz i obrazlagati dobivena rješenja što u konačnici utječe na razvoj kritičkog mišljenja.
Problemske zadatke se treba povezivati s iskustvima učenika iz neposrednog okruženja i aktualnim nastavnim sadržajima ostalih nastavnih predmeta u cilju ostvarenja korelacije.
Sadržaj ove nastavne cjeline može se povezati s međupredmetnim temama Osobni i socijalni razvoj i Poduzetnost.
C
Geometrija i mjerenjaC.V.1 Učenik crta i određuje elemente kuta.
C.V.2 Učenik crta trokut, kvadrat i pravokutnik.
C.V.3 Učenik primjenjuje formulu za opseg trokuta te formule za opseg i površinu pravokutnika i kvadrata za rješavanje problemskih zadataka različitih konteksta.
MTP-3.1.1 MTP-3.1.1 MTP-3.2.1 - opisuje i crta šiljasti, pravi i tupi kut
- koristi oznake za kut, krakove i vrh kuta
- uspoređuje šiljasti, pravi i tupi kut
- određuje pripadnost točke kutu.
- crta raznostranični trokut, pravokutni trokut, pravokutnik i kvadrat
- konstruira jednakostranični i jednakokračni trokut
- označava elemente trokuta, pravokutnika i kvadrata
- određuje mjerljiva obilježja trokuta, pravokutnika i kvadrata.
- računa opseg i površinu pravokutnika i kvadrata
- računa površinu pravokutnog trokuta
- primjenjuje mjerne jedinice za opseg i površinu.
- pravi, šiljasti i tupi kut
- označavanje kuta
- crtanje šiljastog, pravog i tupog kuta
- točke koje pripadaju ili ne pripadaju kutu.
- vrhovi, stranice i kutovi trokuta
- raznostranični, jednakostranični, jednakokračni trokut
- pravokutni trokut
- pravokutnik i kvadrat.
- opseg trokuta, pravokutnika i kvadrata
- površina kvadrata i pravokutnika
- mjerne jedinice za površinu.
Preporuka je stalno ponavljati ključne pojmove i poticati učenike na urednost i pravilnu uporabu pribora za crtanje.
Sadržaj ove nastavne cjeline može se povezati sa sadržajima nastavnih predmeta: Likovna kultura (crtanje), Priroda i društvo (snalaženje u prostoru).
Prave kutove crtati pomoću dva trokuta, a konstrukcije jednakostraničnog i jednakokračnog trokuta raditi pomoću šestara i ravnala.
Duljine stranica prenositi šestarom te poticati učenike na urednost i pravilno korištenje geometrijskog pribora, pribora za pisanje i brisanje.
Sadržaje ove tematske cjeline je moguće povezati sa sadržajima nastavnih predmeta: Hrvatski jezik (jezično izražavanje), Likovna kultura (slikanje, vizualni znakovi), Tjelesna i zdravstvena kultura (poligon).
Uvođenjem kvadratne mreže i ucrtavanjem likova sačinjenih od jediničnih kvadrata učenici će steći predodžbu o pojmu površine plohe.
Određuje površinu kvadrata i pravokutnika korištenjem kvadrata jedinične površine.
U neposrednom okruženju pronaći predmete čije su strane pravokutnici ili kvadrati te im mjeriti dimenzije pa nakon toga računati njihove opsege i površine (školska ploča, stol, bilježnica, udžbenik, zid, ...).
Primjer: Koliko metara ograde treba za ograditi vrt pravokutnog oblika čija je širina 5 metara, a duljina 6 metara?
Sadržaj ove nastavne cjeline može se povezati sa sadržajima nastavnih predmeta: Priroda i društvo (zemljovid), Hrvatski jezik (jezično izražavanje), Likovna kultura (ploha, grafika-otisak).
C.V.4 Učenik konstruira kružnicu i krug na temelju zadanih elemenata.
C.V.5 Učenik primjenjuje računanje volumena kocke i kvadra pri rješavanju problemskih zadataka različitih konteksta.
MTP-3.1.1 MTP-3.1.2 - opisuje kružnicu i krug
- konstruira kružnicu i krug
- određuje pripadnost točke kružnici i krugu.
- računa volumen kocke i kvadra pomoću formule
- koristi mjerne jedinice za volumen
- primjenjuje računanje volumena kocke i kvadra.
- kružnica
- krug
- središte
- polumjer
- promjer.
- mjerne jedinice za volumen
- volumena kocke
- volumena kvadra.
Razliku između kruga i kružnice možemo objasniti koristeći papirne ili kartonske modele kruga uz objašnjenje da je krug dio ravnine, a crtanjem obrisa kruga na papiru ili ploči približiti pojam kružnice.
Učenike treba poticati na pravilnu upotrebu šestara pri prenošenju duljine polumjera i samom crtanju kružnice.
Sadržaj ove nastavne cjeline može se povezati sa sadržajima nastavnih predmeta: Likovna kultura (crtanje, spektar boja), Tjelesna i zdravstvena kultura (formacije u kretanju i vježbanju).
Učenike upoznati s mjernim jedinicama za mjerenje volumena s kojima će se najčešće susretati pri rješavanju zadataka
i pravilnom imenovanju.
Sadržaj ove nastavne cjeline može se povezati sa sadržajima nastavnih predmeta: Hrvatski jezik (jezično izražavanje), Priroda i društvo (vode u zavičaju), Likovna kultura (oblikovanje u prostoru, arhitektura).
D
Podaci, statistika i vjerojatnostD.V.1 Učenik prikazuje rezultate vlastitih istraživanja.
D.V.2 Učenik opisuje vjerojatnost događaja.
MTP-4.1.1 MTP-4.2.2 - provodi istraživanja prema dogovorenim smjernicama
- prikuplja i razvrstava prikupljene podatke na različite načine
- tumači rezultate istraživanja prikazane tablicama, grafikonom i dijagramom.
- procjenjuje mogućnosti konkretnih događaja
- određuje razinu vjerojatnosti događaja kao siguran, moguć i nemoguć događaj.
- prikupljanje podataka
- razvrstava podataka po kriterijima
- tablica
- grafikon
- dijagram.
- sigurni, mogući i nemogući događaj.
Predmet istraživanja učenika petog razreda može biti poveznica sa sadržajem drugih nastavnih predmeta, npr. Prirode i društva (praćenje vremenskih promjena) Tjelesne i zdravstvene kulture (motorička dostignuća, antropometrijska mjerenja) ili u sklopu projekta koji se realizira u odjelu.
Može se uvesti pojam kružnog grafikona ali pri čitanju podataka ne koristiti pojam postotka. Tumačenjem rezultata prikazanih kružnim grafikonom povezati s pojmovima polovina, trećina, tri četvrtine i sl.
Predmetni sadržaj je moguće korelirati sa skoro svim nastavnim sadržajima iz ostalih predmeta.
Poticati učenike da navedu očekivane ishode nekih događaja, npr. bačena olovka će sigurno završiti na stolu,...moguće je da danas dobijem pet iz matematike jer sam sve zadatke uradio,...nemoguće je da danas otputujem u Japan.
Vjerojatniji, manje vjerojatan ili najvjerojatniji ishod se može pojasniti bacanjem kockica ili igre memorije. Učenike poticati pitanjima na koja trebaju odgovoriti procjenom vjerojatnosti uz argumente kojima će obrazložiti svoj odgovor.
Korelaciju je moguće ostvarivati sa svim nastavnim područjima.
- Osnovno
- VI
Godine učenja i podučavanja predmeta: 6 A Skupovi, brojevi i operacije A.VI.1
A.VI.2
A.VI.3
A.VI.4
A.VI.5
A.VI.6
A.VI.7B Algebra B.VI.1 C Geometrija i mjerenja C.VI.1
C.VI.2
C.VI.3
C.VI.4D Podaci, statistika i vjerojatnost D.VI.1 A
Skupovi, brojevi i operacijeA.VI.1 Učenik prikazuje skupove i primjenjuje odnose među njima za prikaz rješenja problema.
A.VI.2 Učenik koristi prirodne brojeve i broj nula.
A.VI.3 Učenik primjenjuje računske operacije u skupu prirodnih brojeva s nulom pri rješavanju problemskih zadataka različitih konteksta.
MTP-1.1.1 MTP-1.2.2 MTP-1.2.1 MTP-1.1.2 MTP-1.2.1 MTP-1.2.2 - oblikuje i prikazuje skupove (brojeva, podataka) i njihove odnose pomoću Vennovih dijagrama
- određuje broj elemenata skupa
- koristi matematičke simbole u zapisu skupova i njihovih odnosa.
- čita i zapisuje prirodne brojeve
- čita, zapisuje i tumači znakove >, ≤, ≥, <, =, ≠ pri uspoređivanju brojeva u skupu No
- zapisuje dekadske jedinice u obliku potencije s bazom 10 i eksponentom iz skupa No
- pridružuje prirodne brojeve točkama brojevnog pravca i obrnuto
- zaokružuje prirodne brojeve.
- zbraja, oduzima, množi i dijeli brojeve u skupu prirodnih brojeva s nulom procjenjujući rezultate kad god je to moguće
- primjenjuje svojstva računskih operacija i veze među računskim operacijama u skupu prirodnih brojeva s nulom
- izračunava vrijednost brojevnog izraza u skupu prirodnih brojeva s nulom
- rješava problemske zadatke različitih konteksta u skupu prirodnih brojeva s nulom, procjenjujući rezultate.
- pojam skupa
- podskup skupa
- presjek skupova
- unija skupova
- broj elemenata skupa.
- skupovi N i No
- zapis dekadske jedinice u obliku potencije s bazom 10
- prethodnik i sljedbenik prirodnoga broja
- brojevni pravac
- uspoređivanje prirodnih brojeva
- zaokruživanje prirodnih brojeva.
- zbrajanje, pribrojnici, zbroj
- oduzimanje, umanjenik, umanjitelj, razlika
- množenje, faktori, umnožak
- dijeljenje, djeljenik, djelitelj, količnik
- komutativnost, asocijativnost
- distributivnost
- kvadrat prirodnoga broja.
Služeći se primjerima iskustveno bliskim učenicima, oblikovati skupove, podskup, uniju i presjek skupova te ih zapisivati ekvivalentnim matematičkim zapisima i prikazivati grafički Euler - Vennovim dijagramima.
Ispisivati i prebrojavati elemente skupa te uvesti pojam brojnosti skupa ne uvodeći pojam kardinalnosti i kardinalnoga broja.
Uvesti pojamove prazan skup (oznaka,svojstva) i jednakost skupova.
Ako vrijeme i struktura razreda dopuštaju uvesti pojam i matematički zapis razlike skupova.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Priroda (istraživanje prirode, organizacija prirode).
Čitati i zapisivati riječima i znamenkama prirodne brojeve veće od milijun.
Zapisivati višekratnik dekadske jedinice u obliku umnoška prirodnog broja i potencije s bazom 10.
Određivati prethodnike i sljedbenike te neposredni prethodnik i neposredni sljedbenik broja iz skupa prirodnih brojeva s nulom.
Prikazivati rješenja nejednakosti i produžene nejednakosti na brojevnom pravcu.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Informatika (vrste podataka, tekstualni podatci, numerički podatci).
Povezati umnožak dvaju jednakih prirodnih brojeva s pojmom kvadrata prirodnog broja, izbjegavajući pojmove baza i eksponent. Prepoznavati kvadrate prirodnih brojeva do 10.
Izlučivati zajednički faktor u brojevnom izrazu.
U brojevnim izrazima koristiti zagrade i različite računske operacije.
Preračunavati mjerne jedinica.
Razvijati mentalno računanje, procjenu rezultata, te kritičko mišljenje kroz preispitivanje smislenosti dobivenih rezultata.
Koristiti zanimljive zadatke (mozgalice, kvizove,...) za razvijanje znatiželje, ljubavi prema matematici i matematičkih kompetencija općenito.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima međupredmetne teme Poduzetnost (oportunitetni trošak, komparativne prednosti).
A.VI.4 Učenik rastavlja broj na proste faktore i primjenjuje kriterije djeljivosti prirodnih brojeva.
A.VI.5 Učenik analizira svojstva cijelih brojeva.
A.VI.6 Učenik organizira koordinatni sustav na pravcu i koordinatni sustav u ravnini.
MTP-1.2.1 MTP-1.2.2 MTP-1.1.1 MTP-1.2.1 MTP-1.1.2 MTP-1.1.2 - određuje djelitelje i višekratnike prirodnog broja
- primjenjuje djeljivost s 2, 3, 5, 9 i 10
- primjenjuje svojstva djeljivosti zbroja, razlike i umnoška prirodnih brojeva
- rastavlja broj na proste faktore
- određuje najveći zajednički djelitelj i najmanji zajednički višekratnik prirodnih brojeva.
- opisuje skup cijelih brojeva i njegove elemente
- određuje neposredni prethodnik i neposredni sljedbenik cijeloga broja
- određuje suprotni broj i apsolutnu vrijednost cijeloga broja
- uspoređuje cijele brojeve.
- zapisuje uređeni par i opisuje njegova svojstva
- crta i opisuje koordinatni sustav na pravcu i pravokutni koordinatni sustav u ravnini
- pridružuje cjelobrojne koordinate točkama pravokutnog koordinatnog sustava u ravnini i obrnuto
- prikazuje geometrijske likove čiji vrhovi imaju cjelobrojne koordinate u pravokutnom koordinatnom sustavu u ravnini.
- djeljivost prirodnih brojeva
- djelitelj, višekratnik
- djeljivost s 2, 3, 5, 9, 10
- svojstva djeljivosti
- prosti i složeni brojevi
- najveći zajednički djelitelj
- najmanji zajednički višekratnik.
- pozitivni i negativni cijeli brojevi
- skup cijelih brojeva Z
- suprotni brojevi
- apsolutna vrijednost cijeloga broja.
- uređeni par
- pravokutni koordinatni sustav u ravnini (ishodište, jedinična dužina, kvadranti, koordinatne osi)
- koordinata točke (apscisa, ordinata).
Primjenjivati po mogućnosti i djeljivost s 4, 6, 25.
U rastavu broja na proste faktore povezati i prikazati višestruki umnožak istih faktora kao potenciju.
Učenici kroz projektne zadatke mogu koristiti Eratostenovo sito za pronalaženje prostih brojeva, pronaći savršene brojeve i trokutaste brojeve te tako dodatno razvijati znatiželju, istraživački duh i ljubav prema brojevima i matematici općenito.
Razvijati logičko i kritičko mišljenje kroz primjere iz svakidašnjeg života koji se rješavaju primjenom najvećeg zajedničkog djelitelja i najmanjeg zajedničkog višekratnika, preispitujući dobivena rješenja.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima gotovo svih predmeta.
Pojasniti proširivanje skupa prirodnih brojeva do skupa cijelih brojeva i predočiti ta dva skupa Vennovim dijagramima i na brojevnom pravcu.
Obratiti pažnju jesu li učenici usvojili da znak - označava predznak negativnog broja, suprotan broj i znak za računsku radnju oduzimanja.
Poželjno je češće na brojevnom pravcu predočavati neposredni prethodnik i neposredni sljedbenik cijeloga broja, suprotni broj te geometrijsko značenje apsolutne vrijednosti cijeloga broja.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Priroda (pokusi), Geografija (reljef, apsolutna nadmorska visina, depresija) i Povijest (vremenska lenta).
Upoznati učenike o okolnostima nastanka pravokutnog koordinatnog sustava u ravnini i zašto se on naziva i Kartezijev koordinatni sustav u ravnini.
Koordinatni sustav u ravnini uvesti preko prvog kvadranta kroz igre poput Potapanje podmornica, šah ili neke slične računalne igre.
Obratiti pažnju na koordinate točaka koje leže na koordinatnim osima.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Geografija (geografska mreža, geografski smještaj).
A.VI.7 Učenik primjenjuje računske operacije u skupu cijelih brojeva pri rješavanju problemskih zadataka različitih konteksta.
MTP-1.2.1 MTP-1.2.2 - zbraja, oduzima, množi i dijeli u skupu cijelih brojeva
- služi se svojstvima računskih operacija i primjenjuje povezanost računskih operacija u skupu cijelih brojeva
- izračunava vrijednost brojevnih izraza u skupu cijelih brojeva
- rješava problemske zadatke različitih konteksta u skupu cijelih brojeva, procjenjujući rezultate.
- zbrajanje, oduzimanje, množenje i dijeljenje u skupu Z
- rad sa zagradama u skupu Z
- kvadrat cijeloga broja
- brojevni izrazi u skupu Z.
Povezivati računanje s cijelim brojevima sa situacijama iz svakidašnjeg života i razvijati kritičko mišljenje kroz preispitivanje smislenosti dobivenog rješenja.
Pri radu sa zagradama koristiti oba načina računanja, ali izvježbati oslobađanje zagrada radi potreba u algebri.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Priroda (pokusi), Geografija (relativna nadmorska visina), Povijest (vremenska lenta) i sa sadržajima međupredmetne teme Poduzetnost (oportunitetni trošak, poduzetnički potencijal, komparativne prednosti).
B
AlgebraB.VI.1 Učenik primjenjuje jednadžbe s cijelobrojnim koeficijentima pri rješavanju problemskih zadataka različitih konteksta.
MTP-2.2.1 MTP-2.1.3 MTP-2.1.1 - izračunava vrijednost algebarskih izraza u skupu cijelih brojeva
- rješava jednadžbe koje se svode na oblik ax=b u skupu cijelih brojeva
- rješava problemske zadatke različitih konteksta primjenjujući jednadžbe s cijelobrojnim koeficijentima.
- algebarski izraz
- monom
- jednakost
- jednadžba
- jednadžba sa zagradama
- rješenje jednadžbe.
Pojasniti da se jednadžba može shvatiti kao vaga u ravnoteži.
Istaknuti važnost provjere rješenja jednadžbe.
Koristiti problemske zadatke iz svakidašnjeg života koji su bliski učenicima i tako ih motivirati da koriste stečeno znanje i vještine.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima skoro svih predmeta.
C
Geometrija i mjerenjaC.VI.1 Učenik primjenjuje svojstva i odnose skupova točaka u ravnini.
C.VI.2 Učenik konstruira geometrijske likove i opisuje njihove elemente.
C.VI.3 Učenik primjenjuje strategije za izračunavanje opsega i površina geometrijskih likova sastavljenih od kvadrata i pravokutnika.
MTP-3.1.1 MTP-3.1.2 MTP-3.2.1 MTP-3.2.2 - opisuje i crta skupove točaka u ravnini te analizira njihove međusobne odnose
- zapisuje matematičkim zapisom skupove točaka u ravnini i njihove odnose
- opisuje, konstruira i primjenjuje simetralu dužine.
- konstruira kružnicu i opisuje kružnicu i krug i njihove elemente
- opisuje pravokutnik, kvadrat i njihove elemente
- konstruira pravokutnik i kvadrat.
- računa opseg i površinu kvadrata i pravokutnika
- odabire i preračunava mjerne jedinice za duljinu i površinu
- rješava problemske zadatke različitih konteksta primjenjujući opseg i površinu kvadrata i pravokutnika.
- ravnina, točka
- pravac, polupravac, dužina
- duljina dužine
- međusobni položaj dvaju pravaca u ravnini
- polovište dužine
- simetrala dužine.
- kružnica (središte kružnice, polumjer i radijus kružnice, promjer i dijametar kružnice, kružni luk)
- krug (tetiva, kružni isječak, kružni odsječak, polukrug, kružni vijenac)
- pravokutnik
- kvadrat
- dijagonale pravokutnika i kvadrata.
- opseg i površina kvadrata
- opseg i površina pravokutnika
- preračunavanje mjernih jedinica.
Poticati i razvijati pravilno matematičko označavanje i zapisivanje skupova točaka u ravnini i njihovih međusobnih odnosa.
Poticati urednost i preciznost pri crtanju i konstruiranju u geometriji.
Konstrukciju okomice povezati sa simetralom dužine.
Simetralu dužine i njena svojstva učenicima demonstrirati kreativnim matematičkim zadacima i primjerima.
Naglasiti razliku između skiciranja, crtanja i konstrukcije.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Likovna kultura (točka, crta, vrste crta, geometrijski pravilna i nepravilna crta, plohe), Tehnička kultura (tehničko crtanje, kotiranje, tehničko pismo) i Geografija (meridijani, paralele).
Demonstrirati kroz igru crtanje kružnice kako bi učenici lakše usvojili pojam kružnice, središta kružnice i polumjera kružnice.
Ako je moguće učenicima i preko paralelograma uvesti i definirati pravokutnik, kvadrat i romb te istaknuti okomitost dijagonala kod kvadrata i romba.
Koristiti se didaktičkim igrama poput tarzije i drugih sličnih igara i grupnim radom kako bi učenici što bolje usvojili ovu cjelinu.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Likovna kultura (plohe određene bojom i omeđene crtom), Tehnička kultura (tehničko crtanje, pravokutne projekcije) i Geografija (meridijani, paralele).
Vizualno predočiti mjerne jedinice za površinu i odnose među njima.
Povezati kvadrat prirodnog broja s površinom kvadrata i mjernim jedinicama za površinu.
Učenici kroz projektni zadatak u praktičnim primjerima van učionice mogu analizirati složeniji lik (lokalna povijesna građevina, trg, mjesna znamenitost i sl,) koji se može razložiti na pravokutnike i kvadrate te tlocrtu izračunati opseg i površinu.
Sadržaj ove tematske cjeline moguće je korelirati sa sadržajem nastavnog predmeta Tehnička kultura (pravokutna projekcija tijela složenog od dvaju kvadrata).
C.VI.4 Učenik konstruira kutove i analizira njihova svojstva i odnose.
MTP-3.1.2 - opisuje i označava kut i njegove elemente
- crta i mjeri kutove
- određuje mjere susjednih i vršnih kutova te kutova uz presječnicu usporednih pravaca
- opisuje i konstruira simetralu kuta
- konstruira kutove od 30°, 45°, 60°, 90°, 120°.
- kut, mjera kuta
- sukuti, vršni kutovi
- kutovi uz presječnicu usporednih pravaca
- simetrala kuta
- konstrukcija kuta od 30°, 45°, 60°, 90°, 120°.
Matematičkim simbolima zapisivati kut i mjeru kuta.
U razredu vizualno predočiti veličine kutova.
Koristiti se ravnopravno kutnim stupnjevima, kutnim minutama i kutnim sekundama pri izračunavanju veličine nepoznatog kuta.
Uvesti pojam suplementarnih kutova, a po mogućnosti i pojam koplementarnih kutova.
Sadržaje ove tematske cjeline moguće je kolerirati sa sadržajima nastavnog predmeta Geografija (geografska mreža, geografski smještaj).
D
Podaci, statistika i vjerojatnostD.VI.1 Učenik analizira podatke prikazane na različite načine.
MTP-4.1.1 - interpretira podatke prikazane tablicama, stupčastim dijagramima ili drugim grafičkim prikazima
- određuje frekvenciju objekta
- crta stupčasti dijagram u prvom kvadrantu kao prikaz podataka.
- skup podataka
- objekt iz skupa podataka
- frekvencija objekta
- stupčasti dijagram.
Uvesti statistiku i obradu podataka kroz projektni zadatak tako da iz medija potraže, donesu i na satu analiziraju podatke prikazane različitim načinima.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Informatika (vrste podataka, tekstualni podatci, numerički podatci) i Geografija (klima, temperatura i padaline, stupčasti dijagrami) i međupredmetnom temom Poduzetnost (dijagrami).
- Osnovno
- VII
Godine učenja i podučavanja predmeta: 7 A Skupovi, brojevi i operacije A.VII.1
A.VII.2
A.VII.3
A.VII.4
A.VII.5
A.VII.6B Algebra B.VII.1 C Geometrija i mjerenja C.VII.1
C.VII.2
C.VII.3D Podaci, statistika i vjerojatnost D.VII.1 A
Skupovi, brojevi i operacijeA.VII.1 Učenik primjenjuje različite zapise razlomaka.
A.VII.2 Učenik povezuje decimalni broj s razlomkom.
A.VII.3 Učenik koristi decimalne brojeve.
MTP-1.1.2 MTP-1.1.2 MTP-1.1.2 - opisuje razlomak povezujući ga sa slikovnim prikazom
- zapisuje nepravi razlomak u obliku mješovitog broja i obrnuto
- zapisuje dekadski razlomak u obliku postotka i obrnuto
- proširuje i skraćuje razlomak.
- opisuje decimalni broj
- zapisuje decimalni broj u obliku neskrativog razlomka i mješovitog broja i obrnuto
- zapisuje decimalni broj u obliku postotka i obrnuto.
- uspoređuje decimalne brojeve
- zaokružuje decimalne brojeve
- zbraja, oduzima, množi i dijeli decimalne brojeve
- izračunava vrijednost brojevnih izraza s decimalnim brojevima
- zapisuje decimalni broj u znanstvenom obliku i obrnuto
- preračunava mjerne jedinice.
- razlomak (brojnik, nazivnik, razlomačka crta)
- pravi i nepravi razlomak
- mješoviti broj
- dekadski razlomak
- postotak
- proširivanje i skraćivanje razlomaka.
- decimalni broj
- decimalna točka
- decimalni razlomak.
- uspoređivanje decimalnih brojeva
- zaokruživanje decimalnih brojeva (približna vrijednost)
- zbrajanje decimalnih brojeva
- oduzimanje decimalnih brojeva
- množenje decimalnih brojeva
- dijeljenje decimalnih brojeva
- potencija s bazom 10
- znanstveni zapis decimalnog broja.
Tumačiti ekvivalentnost razlomačke crte i računske radnje dijeljenja kao i ulogu brojnika i nazivnika u standardnom zapisu racionalnog broja.
Grafički ili modelom prikazivati razlomke i mješovite brojeve kao dijelove cjeline (kvadrata, kruga, mjerne jedinice, novac, pizza, čokolada).
Poticati učenike da kod skraćivanja razlomaka do neskrativog razlomka skraćuju s najvećim zajedničkim djeliteljem.
Uvesti pojam dekadskog razlomka te postotak , kao i ekvivalent razlomku s nazivnikom 100. Poticati učenike na mentalno povezivanje nekih postotaka s razlomcima (10%, 20%, 25%, 50%, 100%, 200%).
Povezivati decimalne brojeve s drugim zapisima (razlomci, mješoviti brojevi).
Preporučiti korištenje točke kao decimalnog znaka iako upotrebom moderne tehnologije u nekim programskim jezicima decimalnu točku zamjenjuje decimalni zarez (Microsoft Excel).
Poticati učenike da prijelaz iz decimalnog broja u druge oblike mogu izračunavati mentalno (decimalni razlomak, postotak) i obrnuto.
Tumačiti zašto prijelaz iz razlomka u decimalni broj nije uvijek praktičan jer neki razlomci u decimalnom obliku imaju beskonačno mnogo decimala (navesti neke primjere).
Sadržaj ove cjeline moguće je korelirati sa sadržajima međupredmetne teme Poduzetnost (financijska pismenost u realnim životnim situacijama).
Uspoređivati decimalne brojeve, razlomke, mješovite brojeve i prirodne brojeve koristeći produženu nejednakost.
Tumačiti potrebu zaokruživanja decimalnih brojeva u svakodnevnom životu.
Poticati učenike na procjenjivanje smislenosti zaokruživanja decimalnih brojeva (baratanje novcem).
Učenici kroz projektne zadatke mogu istraživati i uspoređivati cijene u trgovini te tako dodatno razvijati znatiželju istraživački duh i ekonomičnost u raspolaganju s novcem.
Sadržaj ove cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Geografija (broj stanovnika po kilometru četvornom, natalitet-mortalitet), Biologija (građa i veličina biljaka i životinja) i međupredmetnom temom Poduzetnost (financijska pismenost).
A.VII.4 Učenik primjenjuje različite zapise racionalnih brojeva.
A.VII.5 Učenik pridružuje racionalne brojeve točkama na brojevnom pravcu i u pravokutnom koordinatnom sustavu i obrnuto.
A.VII.6 Učenik primjenjuje računske operacije u skupu racionalnih brojeva pri rješavanju problemskih zadataka različitih konteksta.
MTP-1.1.2 MTP-1.1.2 MTP-1.2.1 - razlikuje pozitivne i negativne racionalne brojeve i zapisuje racionalan broj u standardnom zapisu
- svodi razlomke na zajednički nazivnik
- uspoređuje racionalne brojeve.
- pridružuje racionalne brojeve točkama na brojevnom pravcu i obrnuto
- pridružuje točku zadanu uređenim parom racionalnih brojeva u pravokutnom koordinatnom sustavu u ravnini i obrnuto.
- zbraja, oduzima, množi i dijeli u skupu racionalnih brojeva
- izračunava vrijednost brojevnih izraza s racionalnim brojevima
- rješava problemske zadatke u različitim kontekstima primjenjujući računske operacije u skupu racionalnih brojeva.
- pozitivni racionalni brojevi
- negativni racionalni brojevi
- proširivanje razlomaka
- skraćivanje razlomaka
- svođenje razlomaka na najmanji zajednički nazivnik
- uspoređivanje racionalnih brojeva.
- brojevni pravac
- suprotni racionalni brojevi
- apsolutna vrijednost racionalnog broja
- pravokutni koordinatni sustav u ravnini (uređeni par, koordinate točke).
- zbrajanje racionalnih brojeva
- oduzimanje racionalnih brojeva
- množenje racionalnih brojeva
- dijeljenje racionalnih brojeva
- recipročni brojevi
- svojstva računskih operacija.
Tumačiti potrebu proširenja skupa cijelih brojeva Z na skup racionalnih brojeva Q kroz primjere iz svakodnevnog života.
Poticati učenika na mentalno uspoređivanje razlomaka jednakih nazivnika, jednakih brojnika i suprotnih predznaka.
Uspoređivati i redati po veličini racionalne brojeve koristeći produženu nejednakost.
Kod prikazivanja na brojevnom pravcu i u pravokutnom koordinatnom sustavu u ravnini koristiti manje nazivnike kako bi dijeljenje jedinične dužine bilo jednostavnije.
Određivati između kojih se cijelih brojeva nalazi zadani razlomak.
Određivati suprotne brojeve i apsolutnu vrijednost racionalnog broja na brojevnom pravcu.
Sadržaj ove tematske cjeline može se povezati sa sadržajima nastavnih predmeta: Geografija i Povijest.
Pri računanju u skupu racionalnih brojeva poticati učenike na skraćivanje razlomaka kad god je to moguće.
Izračunavati vrijednost brojevnih izraza koji uključuju zagrade i više računskih radnji kao i različite zapise racionalnih brojeva.
Poticati učenike na biranje različitih metoda pri rješavanju zadataka.
Sadržaj ove cjeline moguće je korelirati sa sadržajima nastavnog predmeta Geografija (izračunavati BDP), međupredmetnim temama Poduzetnost (opisivati osnovne tržišne zakonitosti) i Upotreba IKT - a.
B
AlgebraB.VII.1 Učenik računa s algebarskim izrazima u skupu racionalnih brojava.
MTP-2.2.1 - pojednostavljuje algebarske izraze
- izračunava vrijednost algebarskih izraza.
- algebarski izrazi
- izračunavanje vrijednosti algebarskih izraza.
Izračunavati vrijednost algebarskog izraza uvrštavanjem nepoznanice (npr. ako su a i b zadani racionalni brojevi, izračunaj vrijednost izraza 3a + 0.5b).
Algebarske izraze pojednostavljivati primjenom svojstava računskih operacija u skupu racionalnih brojeva.
C
Geometrija i mjerenjaC.VII.1 Učenik konstruira trokut i analizira njegova svojstva.
C.VII.2 Učenik konstruira četverokut i analizira njegova svojstva.
C.VII.3 Učenik računa i primjenjuje opseg i površinu trokuta i četverokuta.
MTP-3.1.2 MTP-3.1.1 MTP-3.1.1 MTP-3.1.2 MTP-3.2.1 MTP-3.2.2 - opisuje vrste trokute prema njihovim stranicama i kutovima
- povezuje odnos duljina stranica i veličina kutova trokuta
- primjenjuje svojstva i veze veličina vanjskih i unutarnjih kutova trokuta
- skicira i konstruira trokute koristeći Poučke o sukladnosti trokuta
- konstruira karakteristične točke trokuta.
- opisuje vrste četverokuta
- izračunava zbroj veličina unutarnjih i vanjskih kutova četverokuta
- skicira i konstruira četverokute (paralelograme).
- računa opseg i površinu trokuta i paralelograma
- opisuje i računa opseg i površinu geometrijskih likova sastavljenih od trokuta i paralelograma
- rješava problemske zadatke primjenjujući opseg i površinu trokuta i paralelograma.
- trokut
- vrste trokuta
- vanjski i unutarnji kutovi trokuta
- sukladnost trokuta
- poučci o sukladnosti trokuta
- konstrukcija trokuta
- karakteristične točke trokuta.
- četverokut
- vrhovi, stranice, kutovi i dijagonale četverokuta
- paralelogram, pravokutnik, kvadrat, romb, trapez
- unutarnji i vanjski kutovi četverokuta
- konstrukcija četverokuta.
- opseg i površina trokuta
- opseg i površina paralelograma
- opseg i površina romba
- opseg i površina pravokutnika
- opseg i površina kvadrata.
Povezivati vanjske i unutarnje kutove kao i dva unutarnja i nasuprotni vanjski kut.
Pri konstrukciji i crtanju trokuta inzistirati na crtanju skice trokuta i planiranju konstrukcije pomoću Poučaka o sukladnosti trokuta.
Prema mogućnosti koristiti digitalne alate za crtanje trokuta (Geogebra).
Učenici kroz projektni zadatak "Fraktali" mogu dodatno razvijati preciznost, urednost i strpljivost u izradi složenijih zadataka kao i smisao za estetiku.
Sadržaj ove cjeline moguće je korelirati sa sadržajima nastavnog predmeta Likovna kultura (Ploha, ritam, kompozicija geometrijskih likova).
Pri klasifikaciji četverokuta inzistirati na uočavanju zajedničkih osobina i razlika među četverokutima.
Pri konstrukciji i crtanju četverokuta inzistirati na crtanju skice četverokuta i planiranju konstrukcije.
Prema mogućnosti koristiti digitalne alate za crtanje četverokuta (Geogebra).
Učenici kroz projektni zadatak "Tepih Sierpinskog" mogu dodatno razvijati preciznost, urednost, smisao za estetiku kao i sposobnosti rada u timu.
Sadržaj ove cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Likovna kultura (Ploha, ritam, kompozicija geometrijskih likova) i Tehnička kultura (crtanje tlocrta).
Izračunavati opseg i površinu nestandardnog geometrijskog lika podjelom na trokute i paralelograme i pomoću kvadratne mreže.
Izračunavanje opsega i površina paralelograma uključuje pravokutnik, kvadrat i romb.
Poticati učenike na procjenu opsega i površina standardnih i nestandardnih geometrijskih likova kad god je to moguće.
Sadržaj ove cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Tehnička kultura i Geografija (izabirati prikladne mjerne jedinice za površinu i duljinu).
D
Podaci, statistika i vjerojatnostD.VII.1 Učenik prikazuje i tumači prikupljene podatke.
MTP-4.1.2 MTP-4.1.1 - prikuplja, obrađuje i prikazuje prikupljene podatke
- određuje i primjenjuje aritmetičku sredinu
- tumači i prezentira podatke prikazane na različite načine.
- podaci
- frekvencija
- dijagram
- aritmetička sredina.
- linijski dijagram
Kreirati anketne listiće i provoditi različite ankete na razini razreda ili škole i podatke prikazati tablično, stupčastim ili linijskim dijagramom.
Izračunavati i primjenjivati aritmetičku sredinu različitih podataka prikazanih tablično ili dijagramom (zaključne ocjene, cijena proizvoda u različitim trgovinama, količina padalina kroz godinu, temperatura kroz godinu, itd).
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Informatika (prikazivanje podatka uz pomoć različitih informatičkih alata), Biologija (ekološki otisak), Geografija (klima, temperatura i padaline) i sa sadržajima međupredmetne teme Poduzetnost (promjena cijena).
- Osnovno
- VIII
Godine učenja i podučavanja predmeta: 8 A Skupovi, brojevi i operacije A.VIII.1 B Algebra B.VIII.1
B.VIII.2
B.VIII.3
B.VIII.4
B.VIII.5C Geometrija i mjerenja C.VIII.1
C.VIII.2
C.VIII.3
C.VIII.4
C.VIII.5
C.VIII.6D Podaci, statistika i vjerojatnost D.VIII.1 A
Skupovi, brojevi i operacijeA.VIII.1 Učenik primjenjuje postotni račun pri rješavanju problemskih zadataka različitih konteksta.
MTP-2.1.3 - mentalno određuje vrijednost i značenje postotaka 100%, 50%, 10%, 20%, 25%, 1%
- računa postotni iznos, postotak i osnovnu vrijednost odabirući najprikladniju strategiju
- rješava problemske zadatke različitih konteksta primjenjujući postotni račun.
- postotak, postotni iznos, osnovna vrijednost
- primjena postotaka.
Staviti naglasak na značenje pojma postotka (postotak pokazuje dio cjeline, a ne pokazuje koliko je velika cjelina).
Povezati postotak, proporcionalnost i obrnutu proporcionalnost mijenjajući vrijednosti elemenata postotnog računa. (npr. određujući vrijednost postotka kao dio cjeline od 200, 300, 50,... pokazati da su postotni iznos i osnovna vrijednost proporcionalne veličine).
Izračunavati postotni iznos, postotak i osnovnu vrijednost množenjem ili dijeljenjem, pomoću razmjera (pravilo trojno) i formulom. Nije važan način na koji učenik računa, važno je da razumije odnos veličina u postotnom računu.
Primjerima primjene postotnog računa pokazati kako je matematika u pozadini svakodnevnih zbivanja (sniženje i poskupljenje, PDV, zdravi život, prolaznost na ispitima, izborni rezultati, popunjenost baterije itd.)
Poticati učenike na logičko zaključivanje kako bi mogli kritički procjenjivati informacije u obliku postotaka.
Preporučuje se upotreba IKT-a i edukativnih igara za ponavljanje gradiva.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima međupredmetne teme Poduzetnost (faktori promjene cijene).
B
AlgebraB.VIII.1 Učenik primjenjuje omjere, razmjere, proporcionalne i obrnuto proporcionalne veličine pri rješavanju problemskih zadataka različitih konteksta preispitujući smislenost rješenja.
B.VIII.2 Učenik primjenjuje linearnu ovisnost.
B.VIII.3 Učenik analizira rješenje linearne jednadžbe, linearne nejednadžbe i sustava dviju linearnih jednadžbi.
MTP-1.1.1 MTP-1.1.2 MTP-2.2.2 - opisuje omjer i razmjer i određuje nepoznati član razmjera
- opisuje proporcionalne i obrnuto proporcionalne veličine
- prikazuje grafički proporcionalnosti u pravokutnom koordinatnom sustavu
- primjenjuje proporcionalnost i obrnutu proporcionalnost pri rješavanju problemskih zadataka različitih konteksta preispitujući smislenost rješenja.
- zapisuje linearnu ovisnost formulom y = ax + b
- prikazuje linearnu ovisnost tablično i grafički
- primjenjuje linearnu ovisnost pri rješavanju problemskih zadataka različitih konteksta.
- rješava linearnu jednadžbu i raspravlja o egzistenciji rješenja
- rješava linearne nejednadžbe i rješenje prikazuje na brojevnom pravcu
- opisuje sustav dviju linearnih jednadžbi (njegovo rješenje, standardni oblik, ekvivalentne sustave)
- rješava sustav dviju linearnih jednadžbi metodom supstitucije i provjerava točnost rješenja
- rješava sustav dviju linearnih jednadžbi metodom suprotnih koeficijenata i provjerava točnost rješenja
- raspravlja o egzistenciji rješenja sustava dviju linearnih jednadžbi.
- omjeri
- razmjeri
- proporcionalne veličine i njihova primjena
- grafički prikaz proporcionalnosti
- obrnuto proporcionalne veličine i njihova primjena.
- linearna ovisnost
- grafički prikaz linearne ovisnosti
- linearna jednadžba i nejednadžba
- nemoguće i neodređeno rješenje jednadžbe
- pojam sustava i njegovo rješenje
- metoda supstitucije
- metoda suprotnih koeficijenata.
Raditi omjere istovrsnih veličina kao i omjere raznovrsnih veličina uz koje treba pisati mjerne jedinice. Mogu se, ako situacija dopušta, raditi i produženi omjeri.
Navoditi primjere omjera iz svakodnevnog života (miješanje boja, nasljedstvo, zemljovid, itd.).
Rješavati zadatke s proporcionalnim i obrnuto proporcionalnim veličinama koristeći razmjer (pravilo trojno).
Poticati kritičko mišljenje pri rješavanju problema iz proporcionalnosti i obrnute proporcionalnosti.
Kroz projektni zadatak učenici mogu istražiti omjer zlatnog reza (napraviti model zlatnog šestara).
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (Mehanika), Geografija (prikazivanje Zemljine površine), Likovna kultura (proporcije i omjeri - zlatni rez) i međupredmetnom temom Poduzetnost (odnos troškova i prihoda, tržišna ravnoteža).
Staviti naglasak na proučavanje međusobno ovisnih veličina, zapisivanje linearne ovisnost algebarski, tablično i grafičkim prikazom.
Više poticati logičko razmišljanje i sposobnost analize problema, nego tehniku računanja.
Preporučuje se upotreba programa dinamičke geometrije (Geogebra) za grafički prikaz linearne ovisnosti.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (kinematika - grafovi gibanja) i Informatika.
Ponoviti rješavanje linearnih jednadžbi koje se svode na oblik ax=b u skupu cijelih brojeva.
Prije primjene metode za rješavanje sustava sustav svesti na standardni oblik.
Rješenje sustava uvijek napisati kao uređeni par.
Preporučuje se upotreba IKT-a za provjeravanje točnosti rješenja.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Fizika (izračunavanje nepoznate fizikalne veličine rješavanjem linearne jednadžbe).
B.VIII.4 Učenik primjenjuje linearnu jednadžbu i sustav dviju linearnih jednadžbi pri rješavanju problemskih zadataka različitih konteksta.
B.VIII.5 Učenik analizira međusobne odnose pravaca u koordinatnoj ravnini.
MTP-2.2.1 MTP-2.2.2 MTP-2.2.1 - povezuje eksplicitni i implicitni oblik jednadžbe pravca
- određuje jednadžbu pravca kroz jednu točku i jednadžbu pravca kroz dvije točke
- ispituje pripadnost točke pravcu
- određuje jednadžbe usporednih pravaca
- rješava problemske zadatke različitih konteksta primjenjujući linearnu jednadžbu i sustav dviju linearnih jednadžbi.
- crta pravce u koordinatnoj ravnini
- grafički rješava sustav dviju linearnih jednadžbi i povezuje rješenje s rješenjem dobivenim nekom od algebarskih metoda
- analizira grafičko rješenje sustava.
- primjena sustava
- jednadžba pravca (eksplicitna i implicitna)
- jednadžba pravca kroz jednu točku
- jednadžba pravca kroz dvije točke
- usporedni pravci.
- grafički prikaz pravca u koordinatnoj ravnini
- presjek pravaca i grafičko rješavanje sustava dviju linearnih jednadžbi.
Pri rješavanju problemskih zadataka učenik bira metodu rješavanja sustava.
Kod određivanja jednadžbe pravca kroz jednu točku primijeniti linearnu jednadžbu, a kod određivanja jednadžbe pravca kroz dvije točke primijeniti sustav dviju linearnih jednadžbi.
Posvetiti pažnju jednadžbama pravaca usporednih s koordinatnim osima.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Fizika (izračunavanje nepoznate fizikalne veličine iz formule).
Crtati pravace pomoću koordinata točaka u kojima pravac siječe koordinatne osi i pomoću koeficijenta smjera.
Po mogućnosti vizualizirati crtanje pravaca u pravokutnom koordinatnom sustavu korištenjem programa dinamičke geometrije.
C
Geometrija i mjerenjaC.VIII.1 Učenik računa s vektorima grafički.
C.VIII.2 Učenik preslikava skupove točaka u ravnini.
C.VIII.3 Učenik primjenjuje svojstva mnogokuta pri rješavanju problemskih zadataka različitih konteksta.
MTP-3.1.1 MTP-3.1.4 MTP-3.1.2 - crta i opisuje vektor
- crta i opisuje jednake i suprotne vektore i nulvektor
- crta i određuje zbroj i razliku kolinearnih i nekolinearnih vektora.
- translatira skupove točaka u ravnini
- crta osnosimetrične skupove točaka u ravnini
- crta centralnosimetrične skupove točaka u ravnini
- rotira skupove točaka u ravnini.
- opisuje mnogokut i njegove elemente (pravilni i nepravilni mnogokut, konveksni i nekonveksni mnogokut)
- računa broj dijagonala i zbroj veličina kutova u mnogokutu
- konstruira pravilne mnogokute i računa im opseg i površinu
- rješava problemske zadatke različitih konteksta primjenjujući svojstva mnogokuta.
- vektor (duljina, smjer, orijentacija), jednaki i suprotni vektori, nulvektor
- zbrajanje vektora (pravilo paralelograma, pravilo trokuta) i svojstva zbrajanja
- oduzimanje vektora
- translacija
- osna simetrija
- centralna simetrija
- rotacija.
- mnogokuti (vrhovi, stranice, kutovi)
- dijagonale mnogokuta
- kutovi mnogokuta
- pravilni mnogokuti
- konstrukcija pravilnih mnogokuta
- opseg i površina mnogokuta.
Kroz primjere pokazati razliku između dužine i vektora, kao i smjera i orijentacije.
Uočiti i zapisivati kolinearne, nekolinearne, jednake i suprotne vektore na paralelogramima, pravilnom šesterokutu, jednakostraničnom trokutu.
Zbrajati i oduzimati vektore na paralelogramima, pravilnom šesterokutu, jednakostraničnom trokutu i u koordinatnoj ravnini.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (Mehanika) i Geografija (smjer gibanja stalnih vjetrova).
Ponoviti karakteristične točke trokuta i primjenjivati ih kod preslikavanja.
Preslikavati geomerijske likove i dizajnirati oblike u koordinatnoj ravnini. Može se, ako situacija dopušta, pokazati kompozicija preslikavanja.
Inzistirati na preciznosti, urednosti, točnosti i upotrebi geometrijskog pribora.
Za preslikavanje skupova točaka u ravnini preporučuje se upotreba IKT-a.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Likovna kultura (ritam i simetrija).
Uočavati mnogokute u učionici, prirodi, itd.
Pri konstrukciji inzistirati na preciznosti, točnosti i upotrebi geometrijskog pribora.
Pri konstrukciji pravilnih mnogokuta (šesterokuta, osmerokuta, dvanaesterokuta) preporučuje se upotreba IKT-a
Učenici kroz projektne zadatke rješavaju probleme prebrojavanja pomoću broja dijagonala u mnogokutu ili kroz projektni zadatak izrađuju plakat u obliku mentalne mape s formulama za opseg i površinu mnogokuta.
C.VIII.4 Učenik primjenjuje Talesov poučak o proporcionalnim dužinama i sličnost trokuta pri rješavanju problemskih zadataka različitih konteksta.
C.VIII.5 Učenik analizira međusobni položaj pravca i kružnice.
C.VIII.6 Učenik primjenjuje svojstva opsega i površine kruga pri rješavanju problemskih zadataka različitih konteksta.
MTP-3.1.1 MTP-3.1.2 MTP-3.1.1 MTP-3.2.1 - opisuje Talesov poučak o proporcionalnim dužinama
- primjenjuje Talesov poučak o proporcionalnim dužinama pri dijeljenju dužine na jednake dijelove i u zadanom omjeru
- opisuje slične trokute i poučke o sličnosti trokuta.
- računa opseg i površinu sličnih trokuta
- rješava problemske zadatke različitih konteksta primjenjujući Talesov poučak o proporcionalnim dužinama i sličnost trokuta.
- određuje međusobni položaj pravca i kružnice.
- određuje odnos i računa veličinu središnjeg i obodnog kuta.
- računa opseg i površinu kruga
- računa duljinu kružnog luka i površinu kružnog isječka
- rješava problemske zadatke u različitim kontekstima primjenjujući svojstva opsega i površine kruga.
- Talesov poučak o proporcionalnim dužinama
- dijeljenje dužine na jednake dijelove i u zadanom omjeru
- sličnost trokuta
- poučci o sličnosti
- opseg i površina sličnih trokuta
- primjena sličnosti.
- međusobni položaj pravca i kružnice (tangenta, sekanta)
- središnji i obodni kut.
- broj
- duljina kružnice i kružnog luka
- površina kruga
- površina kružnog isječka.
Upoznati djecu s anegdotom kako je Tales iz Mileta izmjerio visinu Keopsove piramide.
Može se, ako situacija dopušta, konstruirati sličan trokut uz zadani koeficijent sličnosti.
Kroz projektni zadatak primjenom svojstva sličnih trokuta određivati udaljenosti (visine).
Koristiti se ako je moguće programima dinamične geometrije pri primjeni sličnosti trokuta i Talesovog poučka.
Ponoviti osnovne elemente kruga (središte, polumjer, promjer, tetiva).
Pri konstrukciji tangente preporuča se upotreba programa dinamičke geometrije, ističući da polumjer i tangenta u dirališnoj točci zatvaraju pravi kut.
Ukoliko situacija u razredu dopušta može se pokazati i Talesov poučak o obodnom kutu te analizirati međusobni položaj dviju kružnica u ravnini.
Upoznati učenike da je broj
omjer duljine kružnice i njenog promjera koristeći se raznim didaktičkim materijalima te digitalnim animacijama, interakcijama.
Poticati učenike da istraže broj
.
Upotrebom IKT-a demonstrirati kako površina kružnog isječka ovisi o središnjem kutu.
Ukoliko situacija dopušta može se raditi i površina kružnog vijenca.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Geografija (oblik i veličina Zemlje).
D
Podaci, statistika i vjerojatnostD.VIII.1 Učenik analizira podatke prikazane dijagramima relativnih frekvencija.
MTP-4.1.1 - računa relativnu frekvenciju razvrstanih podataka
- prikazuje relativne frekvencije tablično, stupčastim dijagramom i kružnim dijagramom
- interpretira podatke prikazane raznim vrstama dijagrama.
- relativna frekvencija
- kružni dijagram.
Na primjerima iz života ponoviti frekvenciju podataka i crtanje linijskih i stupčastih dijagrama.
Zbroj relativnih frekvencija uvijek je 1 ili 100% ako je mogućnost izbora jedan odgovor, ako je više odgovora zbroj relativnih frekvencija je veći od 100%.
Za crtanje kružnih dijagrama preporučuje se upotreba nekog od računalnih programa.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Fizika (Mehanika).
- Osnovno
- IX
Godine učenja i podučavanja predmeta: 9 A Skupovi, brojevi i operacije A.IX.1
A.IX.2
A.IX.3B Algebra B.IX.1
B.IX.2C Geometrija i mjerenja C.IX.1
C.IX.2
C.IX.3D Podaci, statistika i vjerojatnost D.IX.1
D.IX.2A
Skupovi, brojevi i operacijeA.IX.1 Učenik primjenjuje računanje s potencijama s racionalnom bazom i cjelobrojnim eksponentom pri rješavanju problemskih zadataka različitih konteksta.
A.IX.2 Učenik računa s drugim korijenom.
A.IX.3 Učenik primjenjuje računanje u skupu realnih brojeva pri rješavanju problemskih zadataka različitih konteksta.
MTP-1.1.1 MTP-1.2.1 MTP-1.2.2 MTP-1.2.1 MTP-1.1.1 MTP-1.2.2 - kvadrira racionalni broj i procjenjuje vrijednost kvadrata.
- zapisuje umnožak kvadrata kao kvadrat umnoška te količnik kvadrata kao kvadrat količnika i obrnuto.
- opisuje potenciju.
- potencira broj cjelobrojnim eksponentom.
- zbraja, oduzima, množi, dijeli i potencira potencije jednakih baza.
- primjenjuje kvadriranje i potenciranje pri rješavanju problemskih zadataka različitih konteksta.
- računa mentalno drugi korijen nenegativnog racionalnog broja koji se može zapisati kao potpuni kvadrat broja do 20.
- procjenjuje cjelobrojni dio vrijednosti drugog korijena.
- pojednostavljuje i izračunava vrijednost izraza s korijenima.
- istražuje i otkriva postupak djelomičnog korjenovanja.
- racionalizira nazivnik.
- prepoznaje odnose među skupovima N, Z, Q, I i R i iskazuje razliku između racionalnog i iracionalnog broja.
- određuje pripadnost rješenja brojevnog izraza skupovima N, Z, Q, I i R.
- prikazuje beskonačni periodični decimalni broj razlomkom i obrnuto.
- uspoređuje realne brojeve.
- crta i očitava točku zadanu realnom koordinatom u koordinatnom sustavu na pravcu i u koordinatnom sustavu u ravnini.
- kvadriranje
- kvadrat umnoška i količnika
- potenciranje (baza, eksponent)
- zbrajanje i oduzimanje potencija
- množenje i dijeljenje potencija
- potencije s negativnim eksponentom
- potenciranje potencija.
- drugi korijen
- zbrajanje i oduzimanje korijena
- množenje i dijeljenje korijena
- djelomično korjenovanje
- racionalizacija nazivnika.
- skupovi N, Z, Q
- skup iracionalnih brojeva
- skup realnih brojeva
- realne koordinate na brojevnom pravcu i u koordinatnom sustavu.
Objasniti učenicima korist i inzistirati na poznavanju kvadrata prirodnih brojeva do 20.
Uvježbati zapisivanje potencije s bazom 10 u obliku razlomka i decimalnog broja i obrnuto.
Objasniti razliku između
i
Ukazati na svakodnevnu potrebu za korištenjem vrlo malih i vrlo velikih brojeva - znanstveni zapis broja te na ovom mjestu obraditi računanje s brojevima zapisanim znanstvenim zapisom.
Navesti povijesne anegdote vezane za potencije kao što je priča o nastanku šaha, zrnima žita i sl.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Fizika (Izražavanje fizikalnih veličina potencijama).
Izbjegavati izračunavanje korijena kojemu je radikand jako veliki broj.
Poticati učenike da objašnjavaju postupke procjenjivanja vrijednosti korijena, djelomičnog korjenovanja, racionalizacije nazivnika i sl.
Naglasiti kako se broj može najbrže djelomično korjenovati rastavljanjem na umnožak dva broja tako da se obuhvati najveći mogući potpuni kvadrat. U suprotnom će se djelomično korjenovanje morati provesti više od jednom.
Objasniti učenicima razliku između
i
, te da zasad ne mogu korjenovati negativne brojeve.
Uputiti učenike da istraže načine izračunavanja drugog korijena.
Nove koncepte pojasniti animacijskim prikazima, geometrijskim ili algebarskim tumačenjima npr. pomoću algebarskih pločica.
Istražiti vezu između rastava nazivnika na proste faktore i decimalnog zapisa broja kroz projektni zadatak.
Rješavati probleme koji uključuju računanje u skupu realnih brojeva. Uspoređivati različite načine rješavanja problema. Utvrđivati smislenost rješenja, raspravljati o utjecaju promjene uvjeta na rješenje problema.
Uključiti i rješavanje mozgalica, zadataka sa šibicama, integrama te svih ostalih zadataka koji potiču razvoj logičkog razmišljanja i zaključivanja. Koristiti se interaktivnim igrama i drugim digitalnim materijalima ako za to postoje uvjeti.
B
AlgebraB.IX.1 Učenik računa s algebarskim izrazima.
B.IX.2 Učenik rješava linearne, kvadratne i jednadžbe s apsolutnom vrijednosti u skupu R.
MTP-2.1.1 MTP-2.2.1 MTP-2.2.2 - kvadrira zbroj i razliku binoma te ih prepoznaje u algebarskim izrazima.
- rastavlja razliku kvadrata na faktore.
- pojednostavljuje algebarske izraze primjenjujući svojstva računskih operacija.
- određuje pripadnost rješenja linearne jednadžbe određenom skupu brojeva.
- rješava jednadžbe s apsolutnom vrijednosti oblika
.
- rješava kvadratnu jednadžbu oblika
.
- kvadrat zbroja i razlike
- razlika kvadrata
- algebarski izrazi
- računanje s algebarskim izrazima.
- linearna jednadžba u skupu R
- linearna jednadžba s apsolutnom vrijednosti
- kvadratna jednadžba oblika
.
Prije kvadriranja binoma upoznati učenike s pravilima kvadriranja monoma pridržavajući se pravila za kvadriranje umnoška i količnika.
Uz obradu formula za kvadrat zbroja i razlike te razlike kvadrata naglasiti da se do rezultata može doći i korištenjem svojstava računskih operacija u algebarskim izrazima.
Poštujući načelo zornosti, kvadrat binoma i razliku kvadrata prikazati slikom i/ili interaktivnim sadržajem.
Pronaći primjere „trikova“ pogađanja brojeva kojima se učenici često znaju zabavljati i objasniti povezanost s algebarskim izrazima. (Npr: Zamisli neki broj. Ja ti dam još toliko. Maja ti dadne još 8. Pola baci u vjetar. Vrati meni moje. To što je ostalo podijeli s 4. Jesi li dobio broj 1? Objasni zašto!).
Prije početka rješavanja kvadratne jednadžbe raspravljati s učenicima o broju i prirodi rješenja jednadžbe.
Izvoditi zaključke o nepostojanju rješenja kvadratne jednadžbe u skupu R.
Rješavati kvadratne jednadžbe oblika
i
.
C
Geometrija i mjerenjaC.IX.1 Učenik primjenjuje Pitagorin poučak i njegov obrat pri rješavanju problemskih zadataka različitih konteksta.
C.IX.2 Učenik opisuje i skicira uspravno geometrijsko tijelo.
C.IX.3 Učenik primjenjuje oplošje i volumen uspravnih geometrijskih tijela pri rješavanju problemskih zadataka različitih konteksta.
MTP-3.2.1 MTP-3.2.2 MTP-3.1.2 MTP-3.1.1 MTP-3.2.2 MTP-3.2.1 - riječima i matematički zapisuje Pitagorin poučak uz zadane oznake na slici i obrnuto.
- izračunava nepoznati element pravokutnog trokuta, kvadrata, pravokutnika, jednakostraničnog trokuta, jednakokračnog trokuta i romba primjenom Pitagorinog poučka.
- rješava problemske zadatke različitih konteksta primjenjujući Pitagorin poučak.
- određuje međusobni položaj pravaca i ravnina u prostoru na modelu kvadra
- opisuje i identificira elemente geometrijskih tijela (baza, pobočke, pobočje, plašt, vrh, brid, visina, plošne i prostorne dijagonale)
- opisuje i crta mrežu prizme, piramide, valjka i stošca.
- računa oplošje uspravnog geometrijskog tijela.
- računa volumen uspravnog geometrijskog tijela.
- rješava problemske zadatke različitih konteksta primjenjujući formule za oplošje i volumen geometrijskog tijela.
- pravokutni trokut (kateta, hipotenuza)
- pitagorin poučak
- obrat Pitagorina poučka
- izračunavanje duljina stranica pravokutnog trokuta
- primjena Pitagorina poučka na pravokutnik, kvadrat, jednokračni trokut, jednakostranični trokut i romb.
- mežusobni položaj pravaca i ravnina u prostoru
- poliedri i rotacijska tijela
- mreža geometrijskog tijela
- prizma
- kocka
- kvadar
- piramida
- valjak
- stožac.
- oplošje i volumen kocke
- oplošje i volumen kvadra
- oplošje i volumen prizmi
- oplošje i volumen valjka
- oplošje i volumen piramida
- oplošje i volumen stošca.
Osim algebarskim tumačenjima, poželjno je nove koncepte pojasniti animacijskim prikazima -posebno dokaz Pitagorinog poučka. Poslužiti se interakcijama i/ili dokazima bez riječi.
Inzistirati na crtanju skice pri rješavanju zadataka.
Ukoliko situacija u učionici dopusti učenicima se može pokazati primjena Pitagorinog poučka na trapez.
Projektnim zadacima približiti učenicima nastavne sadržaje; Pitagorino stablo, Pitagorine trojke, Pitagorejci i Pitagorina biografija, Egipatski i indijski trokut, Spirala drugog korijena itd…
Sadržaj ove tematske cjeline moguće je korelirati sa sadržajem nastavnog predmeta Povijest (Grčka znanost i kultura).
Promatrati tijela oko sebe i određivati radi li se o poliedru ili rotacijskom tijelu.
Radi zornijeg prikaza, koristiti žičane i druge modele geometrijskih tijela.
Crtati skice geometrijskih tijela počevši od baze nacrtane u kosoj projekciji.
Valjak i stožac predstaviti učenicima kao rotacijska tijela te im objasniti kako su nastala.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Fizika (Uvod u fiziku).
Poticati učenike da oplošje i volumen računaju pomoću crteža mreže, skice tijela te da ne uče formule napamet.
Volumen izražavati preko broja jediničnih kocaka (mm3,cm3,dm3, m3,…) te objasniti odnos sa litrom.
Kada je moguće, prije računanja napraviti procjenu.
Volumen piramide objasniti demonstracijom pokusa s tekućinom ili prezentacijom pomoću digitalnih alata.
Ukoliko situacija u učionici dozvoli, učenici se mogu upoznati s formulama za oplošje i obujam kugle.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog premeta Fizika (Fizika, društvo i tehnologija).
D
Podaci, statistika i vjerojatnostD.IX.1 Učenik primjenjuje vjerojatnost slučajnog događaja pri rješavanju problemskih zadataka različitih konteksta.
D.IX.2 Učenik interpretira podatke povezane s novcem.
MTP-4.1.2 MTP-4.2.2 MTP-4.1.1 MTP-4.2.1 - opisuje i procjenjuje vjerojatnost slučajnog događaja kao broj veći ili jednak 0, a manji ili jednak od 1.
- računa vjerojatnost slučajnog događaja.
- rješava problemske zadatke različitih konteksta primjenjujući svojstva vjerojatnosti slučajnog događaja.
- koristi se tečajnom listom i preračunava valute.
- opisuje pojam kamate na štednju i kamate na kredit na primjeru iz stvarnoga života.
- računa kamatu, glavnicu, vrijeme i kamatnu stopu.
- uvod u vjerojatnost
- teorijska i emprijska vjerojatnost.
- tečajna lista, preračunavanje valuta
- osnovni pojmovi poslovanja banaka
- vrste štednje
- vrste kredita
- kamatni račun.
Za bolje razumijevanje vjerojatnosti dobro je izvoditi pokuse (bacanje novčića, izvlačenje kuglica, bacanje kockica).
Kroz pokuse će učenici prikupljati i klasificirati podatke, prebrojavati ih te na kraju izračunati vjerojatnost.
Varijacije bez ponavljanja i s ponavljanjem mogu se odraditi i prebrojavanjem.
Poželjno je koristiti stvarne podatke (iz novina, reklamnih letaka ili mrežnih stranica banaka i sl.)
Potaknuti na učenike da izrađuju vlastite financijske proračune kako bi što odgovornije postupali s džeparcem.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima međupredmetne teme Poduzetnost (bilanca stanja i bilanca uspjeha).
- Srednje
- I
Godine učenja i podučavanja predmeta: 10 A Skupovi, brojevi i operacije A.I.1
A.I.2B Algebra B.I.1
B.I.2
B.I.3
B.I.4
B.I.5
B.I.6C Geometrija i mjerenja C.I.1
C.I.2D Podaci, statistika i vjerojatnost D.I.1 A
Skupovi, brojevi i operacijeA.I.1 Učenik koristi osnovne simbole matematičke logike i računa sa skupovima.
A.I.2 Učenik primjenjuje računanje u skupu realnih brojeva.
MTP-1.1.1 MTP-1.2.1 MTP-1.2.2 - koristi matematičke simbole, pojmove i operacije matematičke logike
- definira i simbolima označava osnovne pojmove vezane za skupove
- zapisuje skupove na različite načine
- računa uniju, presjek i razliku skupova.
- opisuje prirodne, cijele, racionalne i iracionalne brojeve
- predstavlja realne brojeve na brojevnom pravcu
- računa u skupu realnih brojeva poštujući redoslijed i svojstva računskih operacija
- primjenjuje postotni račun, proporcije i aritmetičku sredinu pri rješavanju problemskih zadataka različitih konteksta.
- matematički simboli, matematički pojmovi koji se ne definiraju, definicije, aksiomi, propozicije, teoremi (poučci) i dokazi
- operacije matematičke logike (iskaza)
- skup
- Euler-Vennov dijagram, element skupa, kardinalni broj skupa, prazan skup
- operacije sa skupovima
- Kartezijev umnožak skupova.
- prirodni brojevi, djeljivost, prosti brojevi, najveći zajednički djelitelj, najmanji zajednički višekratnik
- cijeli brojevi
- racionalni brojevi, gustoća skupa racionalnih brojeva
- iracionalni brojevi
- realni brojevi
- svojstva realnih brojeva
- brojevni pravac
- postotci
- aritmetička sredina
- proporcionalne veličine.
Upoznati učenike s podjelom matematičkih simbola: konstante, varijable, znaci matematičkih operacija, znaci matematičkih relacija, kvantifikatori i ostali simboli.
Opisati osnovne (temeljne) pojmove koje ne definiramo i izvedene pojmove koje definiramo. Opisati tvrdnje koje ne dokazujemo (aksiomi) i tvrdnje koje dokazujemo (teoremi ili poučci).
Definirati osnovne operacije matematičke logike: konjunkcija, disjunkcija, implikacija, ekvivalencija i negacija.
Skupove prikazati na različite načine: nabrajanjem elemenata, opisivanjem općeg elementa skupa, Euler-Vennovim dijagramom.
Operacije sa skupovima povezati s operacijama matematičke logike (konjunkcija - presjek, disjunkcija - unija).
Inzistirati na pravilnoj i dosljednoj upotrebi matematičkih simbola i terminologije.
Pri računanju sa skupovima ne treba inzistirati na složenim zadatcima, već na razumijevanju i primjeni pravila.
Sadržaj ove tematske cjeline od naročitog je značaja za precizno i točno matematičko izražavanje u daljem tijeku matematičkog obrazovanja, a može se korelirati sa sadržajem nastavnog predmeta Informatika (logičke operacije u binarnoj aritmetici).
Prlikom proširivanja skupa prirodnih brojeva sve do skupa realnih brojeva potrebno je objasniti povijesne razloge za ta proširenja, uvjetovana potrebom za zatvorenošću skupa u odnosu na osnovne računske operacije.
Preporuča se upotreba IKT-a pri pronalaženju prostih brojeva i provjere djeljivosti prirodnih brojeva.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajem nastavnih predmeta: Informatika (algoritmi za rad s cijelim brojevima, algoritam za nalaženje najvećeg odnosno najmanjeg broja, algoritam koji provjerava je li broj prost ili složen), Kemija (postotci) te međupredmetnom temom Poduzetnost.
B
AlgebraB.I.1 Učenik primjenjuje potencije s cjelobrojnim eksponentom.
B.I.2 Učenik računa s algebarskim izrazima i s algebarskim razlomcima.
B.I.3 Učenik koristi koordinatni sustav u ravnini.
MTP-2.1.1 MTP-2.1.1 MTP-2.2.1 - računa vrijednosti brojevnih izraza koji sadrže potencije s cjelobrojnim eksponentom
- primjenjuje operacije zbrajanja i oduzimanja te množenja i dijeljenja potencija i potenciranje potencija
- koristi znanstveni zapis realnog broja.
- pojednostavljuje algebarske izraze
- primjenjuje formule za kvadrat i kub binoma, razliku kvadrata, razliku i zbroj kubova
- rastavlja na faktore algebarske izraze
- računa s algebarskim razlomcima (skraćuje, množi, dijeli, zbraja i oduzima).
- crta i interpretira skup točaka u koordinatnoj ravnini
- primjenjuje formule za udaljenost dviju točaka, površinu trokuta, polovište dužine.
- pojam potencije
- računanje s potencijama
- znanstveni zapis realnog broja.
- algebarski izrazi
- kvadrat i kub binoma
- razlika kvadrata i razlika i zbroj kubova
- rastavljanje na faktore
- algebarski razlomci
- skraćivanje algebarskih razlomaka
- računske operacije s algebarskim razlomcima.
- koordinatni sustav u ravnini
- udaljenost dviju točaka
- površina trokuta
- polovište dužine.
Istaknuti primjere potenciranja negativnog broja kao i potenciranja umnoška i kvocijenta.
Inzistirati na poznavanju pravila potenciranja te naglasiti da se mogu zbrajati samo potencije jednakih baza i eksponenata.
Kroz primjere problemskih zadataka različitih konteksta primijeniti potencije i zapisivati znanstvenim zapisom (npr. Udaljenost između dva grada na karti koja je u omjeru 1:3 000 000 iznosi 21.2 cm. Kolika je stvarna udaljenost?).
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (znanstveni zapis realnog broja), Informatika (pretvorba brojeva iz jednog brojevnog sustava u drugi, binarna aritmetika), Geografija (prikazivanje zemljine površine).
Odraditi nekoliko primjera nalaženja zajedničkog višekratnika algebarskih izraza.
Poželjno je učenicima pokazati faktorizaciju kvadratnog trinoma rastavljanjem srednjeg člana i inzistirati na njezinom usvajanju.
Sadržaj ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Informatika (korištenje matematičkih izraza u izradi algoritama), Fizika (izračunavanje nepoznate fizikalne veličine u jednadžbama).
Voditi računa da su učenici već upoznati s prikazom točaka u koordinatnom sustavu te će proširiti stečena znanja uvođenjem formula za udaljenost točaka, polovište dužine i površinu trokuta zadanog koordinatama vrhova.
Po mogućnosti upotrebljavati programe dinamičke geometrije.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Fizika (Mehanika) .
B.I.4 Učenik primjenjuje linearnu jednadžbu i sustav linearnih jednadžbi.
B.I.5 Učenik primjenjuje linearne nejednadžbe i sustave linearnih nejednadžbi.
B.I.6 Učenik modelira linearnom funkcijom.
MTP-2.1.1 MTP-2.2.3 MTP-2.2.2 MTP-2.2.3 MTP-1.1.2 - rješava jednadžbe s nepoznanicom u nazivniku svođenjem na linearnu jednadžbu
- izražava traženu veličinu iz zadane formule
- diskutira rješenja linearnih jednadžbi s parametrom
- rješava sustave linearnih jednadžbi odabirući najprikladniju metodu
- rješava linearne jednadžbe s apsolutnim vrijednostima
- primjenjuje linearnu jednadžbu i sustav linearnih jednadžbi u problemskim zadacima različitih konteksta.
- koristi oznake intervala
- zapisuje podskupove skupa realnih brojeva intervalima i prikazuje ih na brojevnom pravcu
- rješava linearne nejednadžbe i sustave linearnih nejednadžbi
- rješava linearne nejednadžbe s apsolutnim vrijednostima.
- računa funkcijske vrijednosti linearne funkcije
- prikazuje linearne funkcije formulom, tablično i grafički
- interpretira graf linearne funkcije
- prikazuje grafički funkciju apsolutne vrijednosti
- modelira linearnom funkcijom u problemskim zadacima različitih konteksta.
- linearne jednadžbe
- linearne jednadžbe s parametrom
- sustav linearnih jednadžbi
- linearne jednadžbe s apsolutnim vrijednostima
- problemski zadaci.
- uređaj u skupu realnih brojeva
- linearne nejednadžbe
- sustav linearnih nejednadžbi
- nejednadžbe s apsolutnim vrijednostima.
- pojam funkcije
- graf linearne funkcije
- graf funkcije apsolutne vrijednosti
- primjena linearne funkcije.
Rješavajući parametarske jednadžbe raspravljati o postojanju rješenja jednadžbe ovisno o parametru kroz primjere ovog tipa:
Primjer: Uz raspravu o ovisnosti rješenja o realnom parametru k riješi jednadžbu:
Povezati računski dobiveno rješenje sustava jednadžbi s grafički dobivenim rješenjem.
Pri tabličnom rješavanju jednadžbi s apsolutnom vrijednošću, ukoliko se ovaj ishod ostvaruje prije B.I.5 voditi računa da učenici još nisu upoznati matematičkim simbolom za beskonačnost niti zapisom nejednakosti pomoću intervala.
Pri rješavanju problemskih zadataka obuhvatiti različita područja kao što su postotci, numerički i geometrijski problemi, problemi smjese, rada, gibanja i drugi.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika i Kemija (primjena u računanju nepoznate fizikalne ili kemijske veličine iz jednadžbe).
Inzistirati da učenici zapisuju rješenja nejednadžbi pomoću intervala i prikazuju ih na brojevnom pravcu. Obratiti pažnju na nejednadžbe koje nemaju rješenja i koje imaju beskonačno mnogo rješenja.
Učenicima pokazati više načina rješavanja linearnih nejednadžbi (rastavljanjem na sustave linearnih nejdnadžbi, tablično te pomoću brojevnog pravca).
Nejednadžbe s apsolutnim vrijednostima oblika |f(x)| <c i |f(x)|>c svoditi na sustave nejednadžbi. Npr. |f(x)| <c zapisujemo -c<f(x)<c.
Sadržaj ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Kemija.
Učenicima uvesti pojam funkcije objašnjavajući pojmove domene, kodomene, zakona preslikavanja i nultočke funkcije.
Naglasiti važnost i ulogu nagiba pravca.
Temeljito obraditi graf funkcije apsolutne vrijednosti oblika f(x)=a|x|+b, f(x)=|x+a|, f(x)=|x+a|+b i objasniti transformacije grafova.
Primjenu linearne funkcije odraditi kroz primjere kao što je:
Marta je planirala putovanje i štedjela je novac godinu dana. Uštedjela je svotu od 1000 KM. Kartu za prijevoz dobila je na poklon. Računala je da joj treba 100 KM dnevno za dnevni smještaj, hranu i izlaske.
a) Koliko dana će najviše provesti na putovanju ako bude trošila prema predviđenom planu?
b) Kad bi dnevni trošak povećala na 120 KM, za koliko dana će skratiti boravak na putovanju?
Sadržaje ovo tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Fizika (sve oblasti fizike).
Preporučuje se upotreba programa dinamičke geometrije.
C
Geometrija i mjerenjaC.I.1 Učenik primjenjuje poučke o sukladnosti i sličnosti trokuta.
C.I.2 Učenik primjenjuje trigonometrijske omjere.
MTP-3.1.1 MTP-3.1.4 MTP-3.1.2 MTP-3.1.4 - analizira položaj karakterističnih točaka trokuta
- primjenjuje Talesov poučak o proporcionalnim dužinama
- koristi koeficijent sličnosti pri računanju opsega i površina sličnih trokuta
- primjenjuje Heronovu formulu
- primjenjuje Euklidov poučak na pravokutni trokut.
- primjenjuje definicije trigonometrijskih omjera pravokutnog trokuta
- računa vrijednosti trigonometrijskih omjera kutova od 30°, 45° i 60°
- računa vrijednosti trigonometrijskih omjera šiljastih kutova koristeći džepno računalo
- primjenjuje trigonometrijske omjere za izračunavanje nepoznatih elemenata jednakokračnog trokuta, pravokutnika, romba, jednakokračnog trapeza i pravilnog mnogokuta.
- sukladnost dužina i kutova
- sukladnost trokuta
- karakteristične točke trokuta
- površina trokuta
- proporcionalnost dužina
- Talesov teorem
- sličnost trokuta i primjena.
- definicija trigonometrijskih omjera šiljastog kuta
- vrijednosti trigonometrijskih omjera kutova 30˚, 45˚ i 60˚
- odnosi među trigonometrijskim omjerima istog kuta
- primjena trigonometrijskih omjera na pravokutni trokut
- primjena trigonometrijskih omjera u planimetriji.
Primijeniti sukladnost u dokazu nekih jednostavnih tvrdnji.
Primjer: Dokažite da su visine spuštene na krakove jednakokračnog trokuta sukladne.
Dokazati Euklidov poučak.
Uz Heronovu formulu korisno bi bilo primijeniti i formule za površinu trokuta izražene pomoću polumjera opisane i upisane kružnice.
Koristeći svojstva sličnosti geometrijskih likova računati nepoznate elemente likova prikazanih slikom.
Po mogućnosti koristiti se programima dinamičke geometrije.
Sadržaje ove cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (kosina) i Likovna umjetnost.
Uočiti važnost pojma sličnosti trokuta pri definiciji trigonometrijskih funkcija.
Uočiti ovisnost promjene vrijednosti sinusa i kosinusa o promjeni kuta. Ova veza se može koristiti kao pomoć u memoriranju vrijednosti trigonometrijskih omjera kutova od 30˚, 45˚ i 60˚.
Koristiti se programom dinamičke geometrije.
Projektni zadatak:
1. Istražiti koliki je kut upada sunčeve svjetlosti za 10 predmeta različite veličine (predmetima morate računati visinu, duljinu sjene i kut upada). S obzirom na visine predmeta diskutirati veličine kutova.
2. Usporediti barem 10 različitih stepenica i izračunati pod kojim se kutom uspinjemo ovisno o njihovoj duljini i širini.
3. Odrediti utjecaj tla i količine svjetla na visinu stabala primjenom trigonometrije (izmjeriti 10 stabala u povoljnim uvjetima i 10 stabala u nepovoljnim uvjetima).
Sadržaj ove cjeline moguće je korelirati sa sadržajima nastavnog predmeta Fizika (kosina).
D
Podaci, statistika i vjerojatnostD.I.1 Učenik prikazuje i analizira podatke.
MTP-4.1.1 MTP-4.1.2 - razlikuje podatke prema obilježju
- prikazuje podatke na različite načine (tablično, histogramom i dijagramima)
- određuje mjere srednje vrijednosti podataka: težinsku aritmetičku sredinu, mod i medijan
- određuje mjere raspršenosti podataka: donji i gornji kvartil te standardnu devijaciju
- crta kutijasti dijagram.
- vrste i prikaz podataka
- mjere srednje vrijednosti
- mjere raspršenja
- kutijasti dijagram (brkata kutija).
Kod grafičkog prikazivanja podataka koristiti sljedeće prikaze: dijagram stablo – list, površinske grafikone te linijske grafikone. Od površinskih grafikona predstaviti stupčaste grafikone (posebno histogram), kružne dijagrame i slikovne dijagrame (piktogram).
Iz različitih grafičkih prikaza čitati podatke i određivati mjere srednje vrijednosti zadanih podataka.
Dobro bi bilo zadati učenicima projektni zadatak u kojima će oni prikupljati određene podatke, a zatim nacrtati stupčasti dijagram relativnih frekvencija za te podatke.
Zadavati primjere u kojima se mogu primijeniti usvojeni pojmovi:
Primjer: Broj krokodila u sedam zooloških vrtova u Aziji je 12, 8, 10, 3, 10, 2 i 9, a broj nilskih konja u istim zoološkim vrtovima je 6, 4, 8, 8, 2, 9 i 5.
a) Prikažite broj krokodila i nilskih konja pomoću dijagrama stablo-list.
b) Odredite srednje vrijednosti te standardne devijacije skupova podataka.
c) Prikažite skupove podataka pomoću kutijastog dijagrama (brkate kutije).
Koristiti se modernom tehnologijom pri računanju i prikazivanju podataka.
Projektni zadatak: Zapisati barem 14 cijena čokolada od 300 grama. Cijene podijeliti u razrede, prikazati ih pomoću stupičastog grafa, grafa stablo-list. Izračunati srednju cijenu, mod i medijan. Koristiti se modernom tehnologijom.
Sadržaj ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Geografija (klimatski dijagrami i stanovništvo), Kemija, Biologija (Ekologija), Fizika (sve oblasti).
- Srednje
- II
Godine učenja i podučavanja predmeta: 11 A Skupovi, brojevi i operacije. A.II.1 B Algebra B.II.1
B.II.2
B.II.3
B.II.4
B.II.5C Geometrija i mjerenja C.II.1
C.II.2
C.II.3
C.II.4D Podaci, statistika i vjerojatnost D.II.1 A
Skupovi, brojevi i operacije.A.II.1 Učenik računa s kompleksnim brojevima i prikazuje ih u Gaussovoj ravnini.
MTP-1.1.2 MTP-1.2.1 - opisuje povezanost skupa realnih i skupa kompleksnih brojeva
- računa s kompleksnim brojevima
- određuje konjugirano kompleksni broj i modul kompleksnog broja
- prikazuje kompleksne brojeve u Gaussovoj ravnini.
- skup kompleksnih brojeva
- računske operacije u skupu kompleksnih brojeva
- konjugirano kompleksni broj
- modul kompleksnog broja
- Gaussova ravnina.
Zaokružiti povijesni razvoj skupova brojeva - od prirodnih do kompleksnih.
Kompleksne brojeve uvesti kao nadgradnju skupa realnih brojeva kroz problemsku situaciju (npr. rješavanje kvadratnih jednadžbi nepotpunog oblika x² +1 = 0; x² + 4 = 0).
U Gaussovoj ravnini interpretirati zbrajanje i oduzimanje kompleksnih brojeva kao i modul kompleksnog broja.
Po mogućnosti se koristiti programima dinamičke matematike za predstavljanje kompleksnih brojeva u Gaussovoj ravnini (GeoGebra).
B
AlgebraB.II.1 Učenik računa s korijenima i potencijama s racionalnim eksponentom.
B.II.2 Učenik primjenjuje kvadratnu jednadžbu, diskriminantu i Vieteove formule.
B.II.3 Učenik grafički prikazuje kvadratnu funkciju i rješava kvadratne nejednadžbe.
MTP-2.1.1 MTP-2.2.1 MTP-2.2.2 MTP-2.2.3 MTP-2.1.2 - računa vrijednosti korijena i potencija s racionalnim eksponentom služeći se džepnim računalom i bez njega
- djelomično korjenuje brojevne i algebarske izraze
- racionalizira nazivnik razlomka
- primjenjuje pravila za računanje s korijenima
- primjenjuje pravila za računanje s potencijama racionalnoga eksponenta.
- rješava potpune i nepotpune kvadratne jednadžbe
- diskutira o prirodi rješenja kvadratne jednadžbe
- primjenjuje Vieteove formule
- faktorizira kvadratni trinom
- rješava jednadžbe koje se svode na kvadratnu
- primjenjuje kvadratnu jednadžbu pri rješavanju problema drugog stupnja.
- analizira oblik kvadratne funkcije u ovisnosti od diskriminante i vodećeg koeficijenta
- određuje nultočke i ekstreme kvadratne funkcije
- grafički prikazuje kvadratnu funkciju
- opisuje tijek kvadratne funkcije
- određuje formulu kvadratne funkcije zadane grafički i tablično
- određuje međusobni položaj pravca i parabole grafički i računski
- rješava kvadratne nejednadžbe i sustave nejednadžbi računski i grafički.
- pojam korijena
- djelomično korjenovanje
- racionalizacija nazivnika
- operacije sa korijenima
- potencije s racionalnim eksponentom.
- kvadratna jednadžba
- formula za rješenja kvadratne jednadžbe
- diskriminanta kvadratne jednadžbe
- Vieteove formule
- faktorizacija kvadratnog trinoma
- jednadžbe koje se svode na kvadratnu
- problemi drugog stupnja.
- kvadratna funkcija
- graf kvadratne funkcije
- nultočke i ekstremi kvadratne funkcije
- pravac i parabola
- kvadratne nejednadžbe.
Treba inzistirati na razumijevanju i primjeni pravila, a ne pretjerivati s količinom i složenosti zadataka.
Kvadrirati binome s drugim i trećim korijenom, npr.
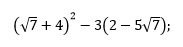
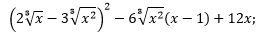
Racionalizirati nazivnik proširivanjem razlomka monomom, te svođenjem nazivnika na razliku kvadrata i kubova, te zbroj kubova, npr. racionalizirati nazivnik razlomaka oblika:
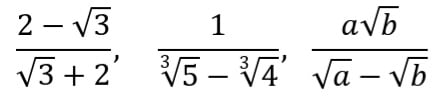 .
.Preoblikovati zapis potencije racionalnoga eksponenta u zapis korijena i obrnuto.
Sadržaj ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (upotreba korijena u fizikalnim formulama, Keplerovi zakoni) i Informatika (matematički izrazi s korijenima kod algoritamskog rješavanja problema).
Nepotpune kvadratne jednadžbe rješavati i bez korištenja formule za rješenja.
Primjenjivati diskriminantu i Vieteove formule u složenijim primjerima jednadžbi s parametrom.
Primjenjivati faktorizaciju kvadratnog trinoma kod jednadžbi s algebarskim razlomcima.
Rješavati jednadžbe koje se svode na kvadratnu: bikvadratne jednadžbe, sustave jednadžbi koji se svode na kvadratnu, jednadžbe višeg reda, iracionalne jednadžbe oblika
 .
.Primjeri raznolike primjene kvadratnih jednadžbi:
1. Polazak autobusa u mjesto udaljeno 30 km odgođen je za 18 minuta. Ako vozač bude vozio prosječnom brzinom 5 km/h većom od uobičajene, stići će na vrijeme. Koliko će u tom slučaju trajati vožnja?
2. Istraživanje je pokazalo da će na jednoj vrsti kruške biti 275 plodova ako je na pola hektara posađeno 25 stabala. Za svako dodatno stablo broj plodova smanjuje se za 5. Koliko je stabala posađeno na pola hektara ako je ukupno dobiveno 7500 plodova?
3. Nađite stranice pravokutnika ako znate razliku duljina njegovih stranica i njegovu površinu. (Babilon)
4. Kvadrat nepoznatog broja uvećan za 21 deset je puta veći od nepoznatog broja. Nađite korijen (rješenje).
Sadržaj ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (različite fizikalne formule, npr. pređeni put u kinematici), Informatika (izrada algoritma za rješavanje kvadratne jednadžbe) i Povijest ( Al-Khwarizmijevo rješenje za nalaženje korijena kvadratne jednadžbe).
Ponoviti pojmove vezane za funkciju.
Ukoliko postoji mogućnost koristiti se programima dinamičke matematike za grafičko predstavljanje kvadratnih funkcija.
Grafički prikazivati prvo funkcije nepotpunog oblika, objasniti translaciju grafa prema sljedećem redoslijedu:
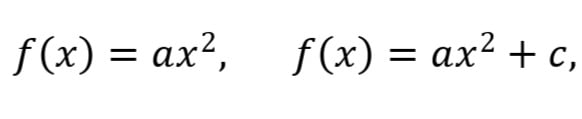
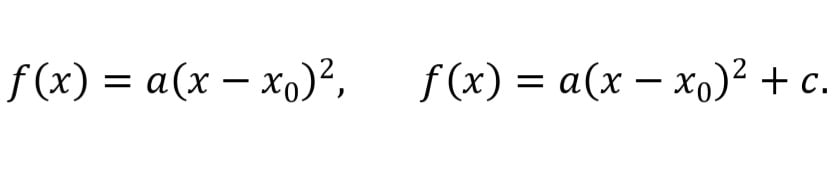
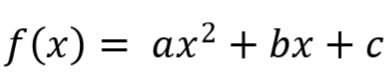
Izvesti formulu za koordinate tjemena parabole. Za grafički prikaz funkcije koristiti se vodećim koeficijentom, nultočkama, tjemenom i sjecištem s osi ordinata.
Rješavati zadatke s parametrom kod kvadratne funkcije, npr.: Za koju vrijednost realnog parametra m, različitog od nule, kvadratna funkcija
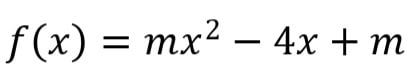 poprima pozitivne vrijednosti za svako x.
poprima pozitivne vrijednosti za svako x.Sadržaj ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (jednoliko ubrzano/usporeno gibanje u kinematici) i Informatika (izrada algoritama za računanje funkcijskih vrijednosti).
B.II.4 Učenik modelira kvadratnom funkcijom.
B.II.5 Učenik analizira algebarske funkcije prikazane analitički i grafički.
MTP-4.1.1 MTP-2.1.2 MTP-2.1.1 - rješava problemske zadatke različitih konteksta primjenjujući maksimalne i minimalne vrijednosti kvadratnih funkcija.
- računa funkcijsku vrijednost uvrštavanjem broja
- određuje domenu, kodomenu i sliku funkcije
- objašnjava bijekciju
- skicira graf inverzne funkcije
- primjene kvadratne funkcije.
- pojam funkcije
- grafički prikaz funkcije
- domena funkcije
- kodomena i slika funkcije
Primjenjivati kvadratnu funkciju u rješavanju problemskih zadataka različitih konteksta, naročito u određivanju najveće i najmanje vrijednosti (najveća zarada, najmanji troškovi, najkraća udaljenost, najveća površina i sl.).
Istaknuti značaj parabole kao krivulje kojom se opisuju različita kretanja (kosi hitac, putanja lopte izbačene prema košu, putanja nogometne lopte...), zatim istaknuti mnoge objekte koji imaju oblik luka parabole (Stari most u Mostaru) i sl.
Mogućnost izrade projektnog zadatka "Primjena parabola u STEM području i umjetnosti" - učenici trebaju pronaći primjere korištenja parabole u prirodnim znanostima, matematici, ekonomiji, tehnici i umjetnosti. Učenike podijeliti u grupe za svaku oblast. Napraviti prezentaciju u kojoj će svaka grupa predstaviti svoje istraživanje.
Primjerima pokazati primjenu kvadratne funkcije u problemskim zadacima različitih konteksta.
Primjer 1: Luk oblika parabole ima raspon 36.5 m, a najveća mu je visina 7.6 m. Odredi visinu luka na udaljenosti 3 m od osi simetrije.
Primjer 2: Koji od pravokutnika opsega 8 cm ima najveću površinu?
Sadržaj ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (kosi hitac, parabola kao graf pređenog puta) i Likovna umjetnost (poznati lukovi u građevinama).
Od algebarskih funkcija analizirati samo:
- polinom prvog i drugog stupnja
- racionalnu funkcija kao kvocijent polinoma nultog, prvog i drugog stupnja
- iracionalnu funkciju kao korijen polinoma prvog i drugog stupnja.Bijekciju prepoznavati i definirati na primjerima funkcija prikazanih Vennovim dijagramima.
Inverznu funkciju skicirati zrcaljenjem s obzirom na pravac y = x.
Grafički i računski određivati funkcijsku vrijednost.
Sliku funkcije određivati računski samo za linearne i kvadratne funkcije.
Pomoću dostupnih alata dinamičke geometrije (ili tablicom pridruženih vrijednosti) obraditi linearne transformacije gore navedenih funkcija.
C
Geometrija i mjerenjaC.II.1 Učenik analizira krug i kružnicu.
C.II.2 Učenik primjenjuje poučak o sinusima i poučak o kosinusu.
C.II.3 Učenik analizira međusobni položaj pravaca i ravnina u prostoru.
MTP-3.1.1 MTP-3.1.2 MTP-3.1.1 MTP-3.2.1 MTP-3.1.1 MTP-3.1.2 - koristi formule za duljinu kružnog luka i površinu kružnog isječka i odsječka
- primjenjuje poučak o obodnom i središnjem kutu
- primjenjuje Talesov poučak o obodnom kutu.
- primjenjuje poučak o sinusima
- primjenjuje poučak o kosinusu
- primjenjuje poučak o sinusima i poučak o kosinusu u planimetriji i problemskim zadacima.
- razlikuje osnovne elemente prostora: točku, pravac i ravninu
- analizira međusobni položaj pravaca i ravnina
- određuje ortogonalnu projekciju točaka u ravnini i prostoru
- određuje kut između pravca i ravnine
- određuje udaljenost točke od pravca i ravnine, te udaljenost pravca i ravnine.
- kružnica i krug
- duljina kružnog luka
- površina kružnog isječka i odsječka
- obodni i središnji kut
- Talesov poučak o obodnom kutu i njegov obrat.
- poučak o sinusima
- poučak o kosinusu
- primjene poučka o sinusima i poučka o kosinusu u planimetriji i problemskim zadacima različitih konteksta.
- točke, pravci i ravnine
- ortogonalna projekcija u ravnini
- ortogonalna projekcija u prostoru
- kut između pravca i ravnine
- udaljenost.
Formule za duljinu kružnog luka i površinu kružnog isječka izvoditi pomoću proporcionalnosti:
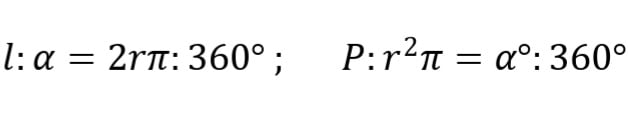
Navoditi učenike da sami dokažu Talesov poučak o obodnom kutu.
Moguće je povezati duljinu kružnog luka s radijanskom mjerom kuta.
Sadržaj ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (kružno gibanje, centripetalna sila) i Likovna umjetnost (Ostwaldov krug kontrasta).
Učenici od ranije koristite definicije i vrijednosti trigonometrijskih funkcija samo za šiljaste kutove pravokutnog trokuta, a poučak o sinusima i poučak o kosinusu treba izvesti i dokazati da vrijedi i za šiljastokutni i tupokutni trokut. Stoga je potrebno uvesti vrijednosti sinusa i kosinusa pravog kuta te sljedeće jednakosti
sin(180°-α)=sinα i cos(180°-α)=-cosα.
Ne preporuča se definiranje trigonometrijskih funkcija na brojevnoj kružnici niti dokazivanje adicijskih formula i formula redukcije jer se ti sadržaji detaljno obrađuju kasnije.
Imati na umu da je u ovom ishodu naglasak na primjeni poučaka o sinusima i o kosinusu pri rješavanju problemskih zadataka različitih konteksta, a relacije među trigonometrijskim funkcijama i trigonometrijski identiteti služe samo u svrhu izvođenja spomenutih poučaka.
Učenike navoditi da u primjenama biraju odgovarajući poučak i da obrazlože svoj izbor.
Povezati poučke s polumjerom opisane kružnice trokuta, s površinom trokuta i s površinom paralelograma.
Primjer:
S vidikovca visine 18 metara bliža obala rijeke vidi se pod kutom depresije
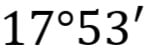 , a druga strana obale pod kutom depresije
, a druga strana obale pod kutom depresije 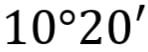 . Koliko je široka rijeka?
. Koliko je široka rijeka?Sadržaj ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Fizika (vektor položaja točke, harmonijski oscilator).
U ovoj cjelini primjenjivati ranije stečena znanja iz trigonometrije. Preporučuje se ishode iz razrade (određuje kut između pravca i ravnine i određuje udaljenost točke od pravca i ravnine te udaljenost pravca i ravnine) ostvariti pri realizaciji ishoda C.II.4.
Po mogućnosti koristiti programe dinamičke matematike radi vizualizacije međusobnog položaja pravaca i ravnina u prostoru.
Sadržaj ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Likovna umjetnost (ortogonalna projekcija točaka) i Geografija (geografski smještaj).
C.II.4 Učenik primjenjuje oplošje i volumen geometrijskih tijela.
MTP-3.1.2 MTP-3.2.1 - definira poliedar, njegovo oplošje i volumen
- opisuje prizmu, piramidu i rotacijska tijela
- računa oplošje i volumen prizme, piramide i rotacijskih tijela
- određuje nepoznate elemente prizme, piramide i rotacijskih tijela.
- pojam poliedra
- oplošje i volumen poliedra
- prizma, oplošje i volumen
- piramida, oplošje i volumen
- rotacijska tijela, oplošje i volumen.
Naglasiti da su riječi obujam i volumen sinonimi. Volumen tumačiti korištenjem Cavalierievog principa.
Po mogućnosti koristiti se programima dinamičke geometrije za zorni prikaz poliedara i nastanak rotacijskih tijela. Kod rotacijskih tijela dati značaj valjku, stošcu i kugli.
Mogućnost izrade projektnog zadatka "Oplošje Platonovih tijela" - učenici trebaju istražiti Platonova tijela i napraviti prezentaciju o njima u kojoj trebaju pojasniti povijesnu ulogu Platona, zatim opisati Platonova tijela (tetraedar, kocka, oktaedar, dodekaedar i ikosaedar), napisati formule za njihovo oplošje i računati ga na nekim primjerima. Učenici mogu raditi u grupama, jedna grupa može pojasniti jedno Platonovo tijelo. Poticati natjecateljski odnos u grupnom radu.
Koristiti znanja iz trigonometrije pri određivanju nepoznatih elemenata geometrijskih tijela.
Primjer:
Uspravna pravilna trostrana piramida ima osnovni brid duljine 6 cm, a pobočni joj je brid duljine 8 cm. Odredi kut koji pobočka zatvara s ravninom baze.
Kao zanimljivost moguće je istaknuti povijesnu poveznicu matematike i arhitekture (Torre pendente di Pisa, Air Force Academy Cadet Chapel, Rotterdam Cube houses, The Glass Cone...)
Sadržaj ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (volumen tijela) i Likovna umjetnost (oblik poliedra u različitim stilovima gradnje kroz povijest), a vidljiv je njezin značaj u tehnici, tehnologiji, kulturi, umjetnosti, i općenito, u problemskim zadacima različitih konteksta.
D
Podaci, statistika i vjerojatnostD.II.1 Učenik primjenjuje vjerojatnost.
MTP-4.2.1 - opisuje slučajan događaj
- primjenjuje algebru događaja za određivanje vjerojatnosti događaja
- računa geometrijsku vjerojatnost
- primjenjuje vjerojatnost kao relativnu frekvenciju.
- događaji
- vjerojatnost događaja
- klasična definicija vjerojatnosti
- geometrijska vjerojatnost
- vjerojatnost kao relativna frekvencija.
Izvoditi eksperimente bacanja igraće kocke, bacanja dviju kockica, kovanog novčića, izvlačenja dviju loptica iz vreće itd.
Provoditi proces istraživanja vjerojatnosti nekog događaja kroz tri različite faze: predviđanje (učenici predviđaju ishod događaja na temelju vlastitih uvjerenja), eksperimentiranje (učenici provode eksperiment kako bi istražili vjerojatnost predviđenog događaja) te zaključivanje (učenici na temelju eksperimenta dolaze do zaključka o vjerojatnosti nekog događaja).
U algebri događaja uraditi uniju, presjek i komplement događaja. Ove operacije prikazivati Vennovim dijagramima i povezati s algebrom skupova.
Sadržaj ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Informatika (prikaz podataka u tablicama, grafikonima i bazama podataka) i Psihologija (istraživanja u psihologiji), a ima i veliku primjenu u problemskim zadacima različitih konteksta (zanimljivo je razmatrati igre na sreću i mogućnost određivanja vjerojatnosti događaja ostvarenja sigurnog dobitka).
- Srednje
- III
Godine učenja i podučavanja predmeta: 12 B Algebra B.III.1
B.III.2
B.III.3
B.III.4
B.III.5
B.III.6
B.III.7C Geometrija i mjerenje C.III.1 D Podaci, statistika i vjerojatnost D.III.1 B
AlgebraB.III.1 Učenik analizira
eksponencijalnu i logaritamsku funkciju prikazanu analitički ili grafički.
B.III.2 Učenik modelira eksponencijalnom i logaritamskom jednadžbom i nejednadžbom.
B.III.3 Učenik analizira trigonometrijske funkcije
prikazane analitički i grafički.
MTP-4.1.1 MTP-2.1.2 MTP-2.2.2 MTP-2.2.3 MTP-2.1.2 MTP-2.1.1 - crta grafove eksponencijalne i logaritamske funkcije
- interpretira zadane grafičke prikaze eksponencijalne i logaritamske funkcije
- primjenjuje eksponencijalnu i logaritamsku funkciju pri rješavanju problemskih zadataka različitih konteksta.
- primjenjuje svojstva potencija i logaritama pri računanju logaritamskih izraza te prelazi iz logaritamskoga u eksponencijalni oblik i obrnuto
- rješava eksponencijalne i logaritamske jednadžbe i nejednadžbe
- primjenjuje eksponencijalne i logaritamske jednadžbe pri rješavanju problemskih zadataka različitih konteksta.
- definira trigonometrijske funkcije realnog broja na brojevnoj kružnici
- primjenjuje svojstva trigonometrijskih funkcija
- računa vrijednosti trigonometrijskih funkcija služeći se džepnim računalom i bez njega
- crta grafove trigonometrijskih funkcija
- interpretira zadane grafičke prikaze trigonometrijskih funkcija.
- eksponencijalna i logaritamska funkcija
- svojstva i graf eksponencijalne i logaritamske funkcije
- primjena eksponencijalne i logaritamske funkcije.
- pojam logaritma i pravila za računanje logaritama
- eksponencijalne i logaritamske jednadžbe
- eksponencijalne i logaritamske nejednadžbe.
- kut
- brojevna (trigonometrijska) kružnica
- definicije trigonometrijskih funkcija
- svojstva trigonometrijskih funkcija
- određivanje vrijednosti trigonometrijskih funkcija
- grafički prikaz trigonometrijskih funkcija.
Potrebno je pri definiranju logaritamske funkcije i crtanju njezinog grafa uvesti pojam inverzne funkcije te uočiti njezine osobine i vezu s grafom eksponencijalne funkcije u odnosu na pravac
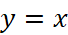 .
.Budući da se svojstvo bijektivnosti funkcije te pojam inverzne funkcije i problem njenog postojanja i određivanja u strogom matematičkom smislu obrađuju tek kasnije, kod uvođenja logaritamske funkcije treba se pobrinuti da učenici shvate logaritamsku funkciju kao funkciju inverznu eksponencijalnoj, u smislu da je to funkcija koja dobivenom broju
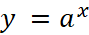 pridružuje početni broj, tj. vraća mu početnu vrijednost.
pridružuje početni broj, tj. vraća mu početnu vrijednost. Može se povući analogija s njima bliskim primjerima inverznih funkcija poput kvadriranja i korjenovanja, sve u svrhu prihvaćanja definicije logaritamske funkcije i njene veze s eksponencijalnom funkcijom, a naglasak treba biti na crtanju grafa, uočavanju njegovih osobina i primjeni ovih funkcija.
Kod grafičkih prikaza eksponencijalne i logaritamske funkcije učenici trebaju odrediti domenu, kodomenu, sliku funkcije, predznak funkcije te monotonost (pad i rast funkcije).
Učenicima zadati projektne zadatke različitih tema vezane za eksponencijalnu i logaritamsku funkciju, npr. računanje jačine potresa, razmnožavanje različitih virusa i bakterija, itd.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Biologija (rast populacije), Kemija (mjerenje pH vodenih otopina, radioaktivni raspad), Geografija (prirast stanovništva) i s međupredmetnom temom Poduzetnost (ekonomska i financijska pismenost).
Koristiti se dostupnim programima dinamičke geometrije kako bi učenici povezali analitička rješenja eksponencijalnih i logaritamskih jednadžbi s grafičkim rješenjem (npr. osim standardnog načina rješavanja jednadžbe
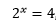 svođenjem na istu bazu pokazat ćemo i njezino grafičko rješavanje nalaženjem sjecišta grafova funkcija
svođenjem na istu bazu pokazat ćemo i njezino grafičko rješavanje nalaženjem sjecišta grafova funkcija 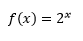 i y = 4 )
i y = 4 )Naglasak treba biti na rješavanju osnovnih eksponencijalnih i logaritamskih nejednadžbi (npr.
 ).
).Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (razina zvuka), Biologija, Kemija te međupredmetnom temom Poduzetnost.
Naglasiti povezanost kuta i duljine luka na brojevnoj kružnici (radijani).
Istaknuti vezu između koordinata točaka na brojevnoj kružnici i trigonometrijskih funkcija sinx i cosx te koordinate točaka na osi tangensa s tgx, osi kotangensa sa ctgx.
Posvetiti pozornost uočavanju svojstava trigonometrijskih funkcija na kružnici (periodičnost trigonometrijskih funkcija, parnost/neparnost) te njihovoj primjeni prilikom računanja vrijednosti trigonometrijskih funkcija.
Poželjno je koristiti programe dinamičke geometrije za demonstraciju grafova trigonometrijskih funkcija kako bi se uočile njihove osobine i svojstva te analizirale iste.
Crtati grafove trigonometrijskih funkcija zaključujući o njihovim svojstvima i promjenama na temelju amplitude, perioda i pomaka.
Iz grafičkog prikaza trigonometrijskih funkcija učenici trebaju odrediti domenu, kodomenu, nultočke te maksimum i minimum (ukoliko oni postoje).
Isticati važnost odabira odgovarajućeg mjerila pri crtanju grafova trigonometrijskih funkcija.
Sadržaje ove tematske cjeline je moguće korelirati sa sadržajima nastavnog predmeta Fizika (valna gibanja i harmonijski oscilator).
B.III.4 Učenik primjenjuje trigonometrijske funkcije
i trigonometrijske jednadžbe.
B.III.5 Učenik primjenjuje jednadžbu pravca.
B.III.6 Učenik primjenjuje jednadžbu kružnice i jednadžbu tangente kružnice.
MTP-2.2.1 MTP-2.1.1 MTP-2.2.2 MTP-2.1.1 MTP-2.1.1 - računa vrijednosti trigonometrijskih funkcija koristeći veze između njih
- pojednostavljuje trigonometrijske izraze korištenjem adicijskih teorema i formula koje proizlaze iz adicijskih teorema
- rješava trigonometrijske jednadžbe
- primjenjuje trigonometrijske funkcije pri rješavanju problemskih zadataka različitih konteksta.
- zapisuje jednadžbu pravca u različitim oblicima i prikazuje pravac u koordinatnom sustavu
- računa koeficijent smjera pravca povezujući ga s kutom koji pravac zatvara s pozitivnim dijelom osi apcisa
- određuje jednadžbu pravca kroz jednu i dvije točke
- određuje jednadžbu pravca iz grafičkoga prikaza
- određuje kut dvaju pravaca
- primjenjuje uvjet paralelnosti i uvjet okomitosti pravaca
- računa udaljenost točke od pravca.
- definira i grafički prikazuje kružnicu
- određuje jednadžbu kružnice iz zadanih elemenata i obrnuto
- prelazi iz općeg oblika jednadžbe kružnice u kanonski oblik
- određuje jednadžbu kružnice iz grafičkoga prikaza
- određuje presjek pravca i kružnice računski i grafički
- primjenjuje uvjet dodira pravca i kružnice
- određuje jednadžbu tangente i normale kružnice u njezinoj točki.
- adicijski teoremi za sinus, kosinus, tangens i kotangens zbroja i razlike
- trigonometrijske funkcije dvostrukog i polovičnog kuta
- trigonometrijske jednadžbe
- primjena trigonometrije.
- jednadžba pravca (eksplicitni, implicitni i segmentni oblik)
- jednadžba pravca kroz jednu točku
- jednadžba pravca kroz dvije točke
- kut dvaju pravaca
- uvjet paralelnosti i okomitosti pravaca
- udaljenost točke od pravca.
- definicija i jednadžba kružnice
- koncentrične kružnice
- međusobni položaj pravca i kružnice
- uvjet dodira pravca i kružnice
- jednadžbe tangente i normale u točki kružnice.
Rješavati trigonometrijske jednadžbe oblika
Asin(Bx+C)+D=0, Acos(Bx+C)+D=0,
Atg(Bx+C)+D=0 i Actg(Bx+C)+D=0.
Voditi računa o području definicije i o pripadnosti rješenja tom području.
Primijeniti trigonometrijske funkcije za modeliranje problemskih situacija različitih konteksta.
Primjer:
Jednoga ljetnoga dana temperatura u pustinji mijenjala se prema formuli

gdje je t vrijeme od 0 do 24 sata, a T temperatura u °C.
a) Kolika je temperatura bila u 9 sati ujutro?
b) U koje je vrijeme poslijepodne temperatura bila 42°C?
c) Kolika je bila najniža temperatura toga dana?
Sadržaje ove tematske cjeline je moguće korelirati sa sadržajima nastavnog predmeta Fizika (valovi).
Obratiti pozornost na zadatke gdje učenici iz grafičkog prikaza trebaju iščitati jednadžbu pravca ili neke elemente, npr. koeficijent smjera, mjeru kuta koju pravac zatvara s pozitivnim dijelom osi apcisa, površinu trokuta koju pravac tvori s koordinatnim osima, itd.
Primjer:
Odredi koeficijent smjera i jednadžbu pravca sa slike ako je kut na slici jednak 120°.
.

Primijeniti formule za udaljenost točke od pravca i mjeru kuta dvaju pravaca na geometrijske zadatke.
Poželjno je koristiti programe dinamičke geometrije kako bi se vizualizirali ključni pojmovi ove cjeline.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Kemija, Fizika (kinematika) i Geografija (geografska mreža).
Potaknuti učenike da nabroje različite odnose između pravca i kružnice kako bi sami zaključili kako doći do uvjeta dodira pravca i kružnice.
Koristiti programe dinamičke geometrije u vizualizaciji odnosa pravca i kružnice te tangente i normale kružnice.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (jednoliko kružno gibanje), Geografija (opseg i veličina Zemlje) i Povijest.
B.III.7 Učenik primjenjuje jednadžbu elipse, hiperbole i parabole.
MTP-2.1.1 - opisuje i grafički prikazuje elipsu, hiperbolu i parabolu
- određuje jednadžbu elipse, hiperbole i parabole iz zadanih elemenata i obrnuto
- određuje jednadžbu elipse, hiperbole i parabole iz grafičkoga prikaza.
- definicija i jednadžba elipse
- definicija i jednadžba hiperbole
- definicija i jednadžba parabole.
Koristiti programe dinamičke geometrije kako bi se zorno prikazao izgled svake krivulje i njezinih elemenata.
Spomenuti povijesnu važnost krivulja iz vremena starih Grka (čunjosječnice) te učenicima zadati projektne zadatke na teme pomrčina Sunca, gibanje nebeskih tijela, itd.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Kemija, Fizika (Keplerovi zakoni), Geografija (sunčev sustav- gibanja Zemlje) i Povijest.
C
Geometrija i mjerenjeC.III.1 Učenik računa s vektorima algebarski i grafički primjenjujući svojstva vektora i operacija s vektorima.
MTP-2.1.1 MTP-3.1.1 - definira vektore i svojstva vektora
- izražava vektor kao linearnu kombinaciju vektora
- prikazuje vektore u koordinatnom sustavu
- izvodi računske operacije s vektorima algebarski i grafički u ravnini i u koordinatnom sustavu
- određuje duljinu vektora
- računa skalarni umnožak vektora
- primjenjuje svojstva skalarnog umnoška.
- definicija i osnovna svojstva vektora
- zbrajanje i oduzimanje vektora
- množenje vektora skalarom
- kolinearni i nekolinearni vektori
- jedinični vektor
- linearna kombinacija vektora
- prikaz vektora u koordinatnom sustavu
- skalarni umnožak vektora
- uvjet okomitosti vektora.
Izvoditi računske operacije s vektorima i njihova svojstva koristiti na primjerima geometrijskih likova u ravnini (trokut, četverokut, pravilni šesterokut) i kasnije u koordinatnome sustavu.
Demonstrirati primjere linearne zavisnosti i nezavisnosti vektora analitički i grafički.
Naglasiti primjenu skalarnog umnoška kod računanju kuta između dva vektora i okomitosti.
Poželjno je koristiti programe dinamičke geometrije kako bi se vizualizirali sadržaji ove tematske cjeline.
Sadržaje ove tematske cjeline je moguće korelirati sa sadržajima nastavnog predmeta Fizika (sila, struja, električno polje).
D
Podaci, statistika i vjerojatnostD.III.1 Učenik primjenjuje osnovne elemente kombinatorike.
MTP-2.1.3 - koristi osnovne principe prebrojavanja
- koristi varijacije, permutacije i kombinacije pri rješavanju problemskih zadataka u različitim kontekstima.
- osnovni principi prebrojavanja
- varijacije bez ponavljanja
- varijacije s ponavljanjem
- permutacije bez ponavljanja
- permutacije s ponavljanjem
- kombinacije bez ponavljanja
- kombinacije s ponavljanjem.
Učenike upoznati s primjerima rješavanja kombinatornih problema gdje se primjenjuju osnovni postupci prebrojavanja ( načelo zbroja i načelo umnoška), varijacije, permutacije i kombinacije.
Za potrebe rješavanja zadataka iz kombinatorike potrebno je definirati binomni koeficijent i faktorijele (sadržaji 4.razreda).
Povezivati značenje broja varijacija, permutacija i kombinacija sa ili bez ponavljanja sa problemskim situacijama različitog konteksta (lutrija, karte, znamenke, raspored sjedenja, itd.).
Pri odabiru odgovarajućeg načela voditi računa je li bitan poredak elemenata i jesu li izabrani svi elementi početnog skupa.
Koristiti ilustracije (gdje je to izvedivo) i programe dinamičke geometrije kako bi se lakše došlo do rješenja nekog kombinatornog problema.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Kemija, Biologija (ekološki otisak, raspršenje) i Psihologija (analiza podataka u psihologiji).
- Srednje
- IV
Godine učenja i podučavanja predmeta: 13 A Skupovi, brojevi i operacije. A.IV.1 B Algebra B.IV.1
B.IV.2
B.IV.3
B.IV.4
B.IV.5
B.IV.6
B.IV.7D Podaci, statistika i vjerojatnost D.IV.1 A
Skupovi, brojevi i operacije.A.IV.1 Učenik analizira svojstva i odnose među skupovima brojeva te računa s kompleksnim brojevima u trigonometrijskom obliku.
MTP-1.1.2 MTP-1.2.1 - analizira skup realnih brojeva
- pretvara kompleksni broj iz algebarskog u trigonometrijski oblik i obrnuto
- zbraja, oduzima, množi, dijeli i potencira kompleksne brojeve u algebarskom i trigonometrijskom obliku koristeći se po potrebi De Moivreovom formulom.
- realni brojevi i njihova svojstva
- skup kompleksnih brojeva
- trigonometrijski oblik kompleksnog broja
- računske operacije u skupu kompleksnih brojeva
- De Moivreova formula.
Prije uvođenja trigonometrijskog oblika kompleksnog broja treba ponoviti algebarski oblik kompleksnog broja te prikaz kompleksnog broja u Gaussovoj ravnini.
Inzistirati na savladavanju računskih operacija s kompleksnim brojevima u algebarskom i trigonometrijskom obliku.
Preporuča se na kreativan način povezati fraktale s kompleksnim brojevima korištenjem IKT-a u obliku nekog projektnog zadatka.
B
AlgebraB.IV.1 Učenik dokazuje tvrdnje matematičkom indukcijom.
B.IV.2 Učenik primjenjuje aritmetički i geometrijski niz.
B.IV.3 Učenik računa limes niza.
MTP-2.1.1 MTP-2.3.2 MTP-2.1.1 MTP-2.1.1 - opisuje postupak matematičke indukcije koristeći induktivan način zaključivanja
- dokazuje matematičke tvrdnje (jednakosti, tvrdnje o djeljivosti)
- računa sa binomnim koeficijentima
- primjenjuje binomnu formulu.
- zapisuje članove niza zadanog početnim članovima ili formulom za opći član niza
- objašnjava pojam aritmetičkog i geometrijskog niza te zapisuje opći član niza
- računa zbroj prvih n članova aritmetičkog i geometrijskog niza
- računa zbroj članova geometrijskog reda
- primjenjuje aritmetički i geometrijski niz pri rješavanju problemskih zadataka različitih konteksta.
- opisuje pojam limesa niza
- razlikuje rastući i padajući niz, konvergentan i divergentan niz
- računa limes niza zadanog općim članom koristeći svojstva limesa.
- princip matematičke indukcije
- primjena matematičke indukcije
- binomni koeficijenti i Pascalov trokut
- binomna formula i njena primjena.
- pojam i zadavanje niza
- opći član i zbroj prvih n članova aritmetičkog niza
- opći član i zbroj prvih n članova geometrijskog niza
- geometrijski red
- kamatni račun.
- monotoni i omeđeni nizovi
- limes niza
- teoremi o limesima.
Kroz primjere upoznati učenike sa induktivnim i deduktivnim načinom zaključivanja.
Preciznim matematičkim jezikom definirati princip i korake matematičke indukcije za dokazivanje tvrdnji koje su istinite za sve prirodne brojeve.
Metodu matematičke indukcije primjenjivati na jednostavnijim jednakostima i tvrdnjama o djeljivosti.
Uvesti binomnu formulu nakon definiranja binomnog koeficijenta i Pascalovog trokuta te posebnu pažnju pridati razumijevanju kraćeg zapisa binomnog teorema.
Sadržaj ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Logika (induktivni i deduktivni načini zaključivanja).
Uvesti nizove nekim svakodnevnim primjerima (npr. niz kuća neke ulice i njihovo numeriranje) te istaknuti da nizovi mogu biti zadani opisno, rekurzivno i formulom za opći član.
Povezati imena nizova s aritmetičkom i geometrijskom sredinom.
Istaknuti primjer određivanja zapisa beskonačnoga periodičnog decimalnog broja u obliku razlomka koristeći sumu geometrijskog reda.
Naglasiti važnost poznavanja jednostavnog i složenog kamatnog računa u svakodnevnom životu.
Spomenuti povijesnu važnost nizova i redova kroz neke primjere kao što su: Fibonaccijev niz, legenda o postanku šaha i Zenonov paradoks o Ahileju i kornjači. Moguće je zadati projektni zadatak povezan s ovim temama.
Koristiti se programima dinamične geometrije (npr. grafičko predstavljanje Fibonaccijevog niza, primjene aritmetičkog i geometrijskog niza).
Sadržaje ove tematske cjeline je moguće korelirati međupredmetnom temom Poduzetnost (npr. organizirati nastavnu aktivnost "Život s kreditom") te sa sadržajima nastavnih predmeta: Biologija (ekologija), Informatika (jednodimenzionalne strukture podataka) i Likovna umjetnost (kompozicija slike).
Ispisivati članove niza na brojevnom pravcu te uočavati postojanje limesa ukoliko se beskonačno mnogo članova tog niza nalazi unutar nekog po volji malog intervala, a konačan broj njih izvan njega.
Prije računanja limesa niza zadanog formulom za opći član, pokušati predvidjeti rješenje raspisivanjem članova niza.
Po mogućnosti se koristiti dostupnim interaktivnim programima i alatima pri vizualizaciji limesa niza na brojevnom pravcu.
B.IV.4 Učenik analizira svojstva funkcija zadanih analitički ili grafički.
B.IV.5 Učenik računa limes funkcije.
B.IV.6 Učenik interpretira i računa derivacije funkcija.
MTP-2.1.1 MTP-2.1.1 MTP-2.1.3 - objašnjava pojmove vezane uz funkcije
- određuje prirodnu domenu i sliku funkcije zadane analitički ili grafički
- prepoznaje bijektivne funkcije
- određuje kompoziciju dviju funkcija
- određuje inverznu funkciju
- skicira graf inverzne funkcije
- crta grafove elementarnih funkcija i ispituje njihova svojstva
- uočava svojstva funkcija promatranjem grafova funkcija.
- računa limes u točki i u beskonačnosti koristeći svojstva limesa funkcija
- određuje neprekidnost funkcije prikazane analitički ili grafički.
- povezuje derivaciju s koeficijentom smjera tangente i brzinom
- izvodi derivaciju linearne i kvadratne funkcije po definiciji
- određuje derivacije funkcija primjenjujući pravila deriviranja
- primjenjuje formulu za derivaciju složene funkcije
- računa derivacije višeg reda.
- pojam i zadavanje funkcije
- domena, kodomena i slika funkcije
- bijekcija
- svojstva funkcija (parnost, periodičnost i monotonost)
- inverzna funkcija
- kompozicija funkcija
- grafički prikazi funkcija.
- limes funkcije
- neprekidne funkcije.
- problem tangente i brzine
- derivacija funkcije u točki
- derivacija zbroja, razlike, umnoška i kvocijenta funkcija
- derivacije elementarnih funkcija
- derivacija složene funkcije
- derivacije višeg reda.
Tražiti precizne definicije pojma funkcije, domene, kodomene i slike funkcije.
Koristiti nazive prirodna domena ili prirodno područje definicije funkcije.
Objasniti kako pomoću vertikalnog testa provjeriti je li neki skup točaka predstavlja graf neke funkcije.
Koristiti horizontalni test za ispitivanje injektivnosti na grafu funkcije. Za ispitivanje surjektivnosti koristiti se činjenicom da je kod surjektivne funkcije slika funkcije jednaka kodomeni.
Skicirati graf inverzne funkcije koristeći činjenicu da su grafovi međusobno inverznih funkcija simetrični u odnosu na pravac y=x.
Po mogućnosti koristiti se programima dinamične geometrije za ponavljanje grafova elementarnih funkcija i njihovih svojstava ili zadati učenicima da ih u bilježnici nacrtaju za domaću zadaću. Ponoviti grafove sljedećih funkcija: linearna, funkcija apsolutne vrijednosti, kvadratna, logaritamska i eksponencijalna, trigonometrijske funkcije.
Upoznati učenike s racionalnom i iracionalnom funkcijom:
.
Po mogućnosti koristiti translacije grafova pri crtanju složenijih grafova.
Predstaviti složenu funkciju preko jednostavnih funkcija. (Primjer: Odredite elementarne funkcije f(x) i g(x) takve da je h(x)=(f∘g)(x) ako je
Kroz projektni zadatak učenici mogu analizirati razvoj funkcija kroz povijest.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Fizika (plinski zakoni, električno polje, mehanika, s-t graf) i Informatika (programiranje).
Prikladno odabrati grafički, tablični ili analitički prikaz funkcija za objašnjenje limesa (granične vrijednosti) funkcije.
Naglasiti da je pojam neprekidnosti povezan uz točke iz prirodne domene
Kroz projektni zadatak učenici mogu istražiti neprekidnost Dirichletove funkcije i signum funkcije.
Preporuča se upotreba IKT-a za bolje razumijevanje limesa i neprekidnosti funkcija.
Po mogućnosti problem tangente predstaviti programom dinamične geometrije.
Pri geometrijskoj interpretaciji derivacije prikazati vezu prirasta varijable i funkcije sa derivacijom u točki.
Spomenuti povijest razvoja diferencijalnog računa.
Po mogućnosti izvesti jedno od pravila deriviranja po definiciji derivacije.
Uz izvod derivacije linearne i kvadratne funkcije po definiciji, upoznati učenike s formulama za deriviranje potencije, trigonometrijskih funkcija, eksponencijalne i logaritamske funkcije.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta Fizika kroz predstavljanje problema brzine.
B.IV.7 Učenik primjenjuje derivacije pri ispitivanju funkcija i crtanju grafa funkcija.
MTP-2.1.3 - određuje jednadžbu tangente i normale u točki grafa funkcije
- određuje intervale monotonosti i ekstreme funkcija koristeći derivacije
- crta grafove polinoma i racionalnih funkcija
- primjenjuje derivacije pri rješavanju problemskih zadataka različitih konteksta.
- tangenta i normala na graf funkcije
- rast i pad funkcije, ekstremi
- tijek funkcije
- crtanje grafa funkcije
- primjene derivacija u problemskim zadacima.
Pri ispitivanju funkcija i crtanju grafova funkcija birati polinome drugog, trećeg ili četvrtog stupnja, a racionalne funkcije takve da u brojniku i nazivniku budu polinomi najviše drugog stupnja.
Utvrditi postupak ispitivanja tijeka funkcije prije grafičkog prikaza: odrediti prirodnu domenu, nultočke (ukoliko postoje), sjecište s osi ordinata, ispitati parnost, odrediti asimptote, odrediti intervale monotonosti i stacionarne točke, odrediti ekstreme (tablično ili pomoću druge derivacije) te popuniti tablicu tijeka funkcije. U ovaj postupak moguće je uvrstiti još dva koraka: tablično odrediti predznak funkcije te pronaći intervale konveksnosti i konkavnosti.
Po mogućnosti vizualizirati crtanje grafova korištenjem programa dinamične geometrije.
Predstaviti primjenu derivacija kroz neke problemske situacije kao što su sljedeći primjeri:
1. Pretpostavimo da neka tvrtka procjenjuje da su ukupni dnevni troškovi izraženi u novčanim jedinicama proizvodnje x komada nekog proizvoda zadani formulom:
a) Odredite derivaciju zadane funkcije i obrazložite što predstavlja ta funkcija.
b) Izračunajte C`(100) i obrazložite rezultat.
2. Od pravokutnog kartona duljina stranica 10 cm i 6 cm napraviti otvorenu kutiju najvećeg volumena.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnih predmeta: Kemija (brzina kemijske reakcije) i Biologija (genetika, ekologija), te međupredmetnom temom Poduzetnost (ekonomska pismenost).
D
Podaci, statistika i vjerojatnostD.IV.1 Učenik tumači i računa vjerojatnost događaja.
MTP-4.2.1 - definira operacije s događajima prikazujući ih Vennovim dijagramima
- koristi vjerojatnosno stablo za izračun vjerojatnosti događaja
- razlikuje zavisne i nezavisne događaje
- računa vjerojatnost događaja koji se ponavljaju
- primjenjuje uvjetnu vjerojatnost.
- prebrojavanje i vjerojatnost
- nezavisnost događaja
- vjerojatnosno stablo
- uvjetna vjerojatnost.
Koristiti vjerojatnosno stablo gdje je god moguće, jer pomoću njega računamo broj mogućih ishoda na pregledan način.
Koristiti tablice ili dijagrame kako bi kreirali prostor elementarnih događaja dvaju nezavisnih događaja.
Primjer: Tri strijelca gađaju metu. Prvi pogađa u 80% gađanja, drugi u 90% , a treći u 75% gađanja. Odredi vjerojatnost da meta bude pogođena točno dva puta?
Spomenuti primjenu vjerojatnosti u igrama na sreću, izračunima vremenske prognoze, usporedbi DNK nizova, računalnim simulacijama itd. Moguće je zadati projektne zadatke uz navedene teme.
Sadržaje ove tematske cjeline moguće je korelirati sa sadržajima nastavnog predmeta: Kemija (pokusi i eksperimenti) i Biologija (ekologija).